Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

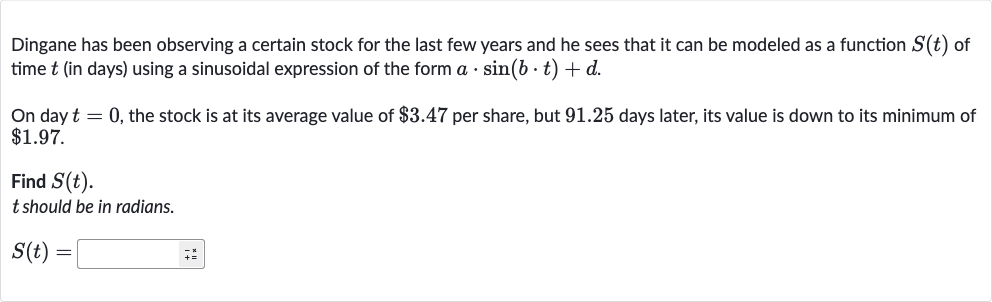
Dingane has been observing a certain stock for the last few years and he sees that it can be modeled as a function
S(t) of time
t (in days) using a sinusoidal expression of the form
a*sin(b*t)+d.
On day
t=0, the stock is at its average value of
$3.47 per share, but 91.25 days later, its value is down to its minimum of
$1.97.
Find
S(t).

t should be in radians.

S(t)=

Dingane has been observing a certain stock for the last few years and he sees that it can be modeled as a function $S(t)$ of time $t$ (in days) using a sinusoidal expression of the form $a \cdot \sin (b \cdot t)+d$ . $\newline$ On day $t=0$ , the stock is at its average value of $\$ 3.47$ per share, but $91$ . $25$ days later, its value is down to its minimum of $\$ 1.97$ . $\newline$ Find $S(t)$ . $\newline$ $t$ should be in radians. $\newline$ $S(t)=$

View step-by-step help

View step-by-step help

Transformations of absolute value functions

Full solution

Q. Dingane has been observing a certain stock for the last few years and he sees that it can be modeled as a function

S(t)

of time

t

(in days) using a sinusoidal expression of the form

a \cdot \sin (b \cdot t)+d

.

\newline

On day

t=0

, the stock is at its average value of

\$ 3.47

per share, but

91

.

25

days later, its value is down to its minimum of

\$ 1.97

.

\newline

Find

S(t)

.

\newline

t

should be in radians.

\newline

S(t)=

Given Average Value: The stock's average value is given at $t=0$ , which is the midline of the sinusoidal function. So $d = \$3.47$ .
Calculate Period: Since the stock reaches its minimum value $91.25$ days later, this corresponds to a quarter of the sinusoidal period. Therefore, the period $P = 91.25 \times 4$ days.
Calculate b: Calculate the value of b, which is related to the period by the formula $b = \frac{2\pi}{P}$ . So $b = \frac{2\pi}{91.25 \times 4}$ .
Calculate Amplitude: The amplitude $a$ is the difference between the average value and the minimum value. So $a = \$3.47 - \$1.97$ .
Calculate $a$ : Calculate the amplitude $a$ . $a = (\$)3.47 - (\$)1.97 = (\$)1.50$ .
Write Function $S(t)$ : Now we have all the parameters to write down the function $S(t)$ . $S(t) = a\sin(b\cdot t) + d$ .
Substitute Values: Substitute the values of $a$ , $b$ , and $d$ into the function. $S(t) = 1.50\cdot\sin\left(\frac{2\pi}{91.25 \cdot 4}\cdot t\right) + 3.47$ .
Simplify Expression for $b$ : Simplify the expression for $b$ . $b = \frac{2\pi}{(91.25 \times 4)} = \frac{2\pi}{365}$ .
Final Function S(t): Write the final function S(t). $S(t) = 1.50\cdot\sin\left(\frac{2\pi}{365}\cdot t\right) + 3.47$ .

More problems from Transformations of absolute value functions

Question

We want to factor the following expression:

\newline

x^{4}+9

\newline

Which pattern can we use to factor the expression?

\newline

U

V

are either constant integers or single-variable expressions.

\newline

1

\newline

(U+V)^{2}

(U-V)^{2}

\newline

(U+V)(U-V)

\newline

(C) We can't use any of the patterns.

Posted 4 months ago

Question

z=-19+3.14 i

\newline

What are the real and imaginary parts of

z

\newline

1

\newline

\newline

\begin{array}{l} \operatorname{Re}(z)=-19 \text { and } \\ \operatorname{Im}(z)=3.14 \end{array}

\newline

\newline

\begin{array}{l} \operatorname{Re}(z)=3.14 i \text { and } \\ \operatorname{Im}(z)=-19 \end{array}

\newline

\newline

\begin{array}{l} \operatorname{Re}(z)=-19 \text { and } \\ \operatorname{Im}(z)=3.14 i \end{array}

\newline

\newline

\begin{array}{l} \operatorname{Re}(z)=3.14 \text { and } \\ \operatorname{Im}(z)=-19 \end{array}

Posted 4 months ago

Question

\begin{array}{l}z=-60-12 i \\ \operatorname{Re}(z)= \\ \operatorname{Im}(z)=\end{array}

Posted 4 months ago

Question

z=-45 i-15.5

\newline

What are the real and imaginary parts of

z

\newline

1

\newline

\newline

\begin{array}{l} \operatorname{Re}(z)=-45 \text { and } \\ \operatorname{Im}(z)=-15.5 \end{array}

\newline

\newline

\begin{array}{l} \operatorname{Re}(z)=-15.5 \text { and } \\ \operatorname{Im}(z)=-45 \end{array}

\newline

\newline

\begin{array}{l} \operatorname{Re}(z)=-45 i \text { and } \\ \operatorname{Im}(z)=-15.5 \end{array}

\newline

\newline

\begin{array}{l} \operatorname{Re}(z)=-15.5 \text { and } \\ \operatorname{Im}(z)=-45 i \end{array}

Posted 4 months ago

Question

z=-12 i+11

\newline

What are the real and imaginary parts of

z

\newline

1

\newline

\newline

\begin{array}{l} \operatorname{Re}(z)=11 \text { and } \\ \operatorname{Im}(z)=-12 \end{array}

\newline

\newline

\begin{array}{l} \operatorname{Re}(z)=11 \text { and } \\ \operatorname{Im}(z)=-12 i \end{array}

\newline

\newline

\begin{array}{l} \operatorname{Re}(z)=-12 i \text { and } \\ \operatorname{Im}(z)=11 \end{array}

\newline

\newline

\begin{array}{l} \operatorname{Re}(z)=-12 \text { and } \\ \operatorname{Im}(z)=11 \end{array}

Posted 4 months ago

Question

(18+4 i)+(-11+23 i)=

\newline

Express your answer in the form

(a+b i)

Posted 4 months ago

Question

(14+60 i)+(-30+2 i)=

\newline

Express your answer in the form

(a+b i)

Posted 4 months ago

Question

(3-91 i)+(67)=

\newline

Express your answer in the form

(a+b i)

Posted 4 months ago

Question

(-71+2 i)+(88-12 i)=

\newline

Express your answer in the form

(a+b i)

Posted 4 months ago

Question

(-33-2 i)-(50+9 i)=

\newline

Express your answer in the form

(a+b i)

Posted 4 months ago