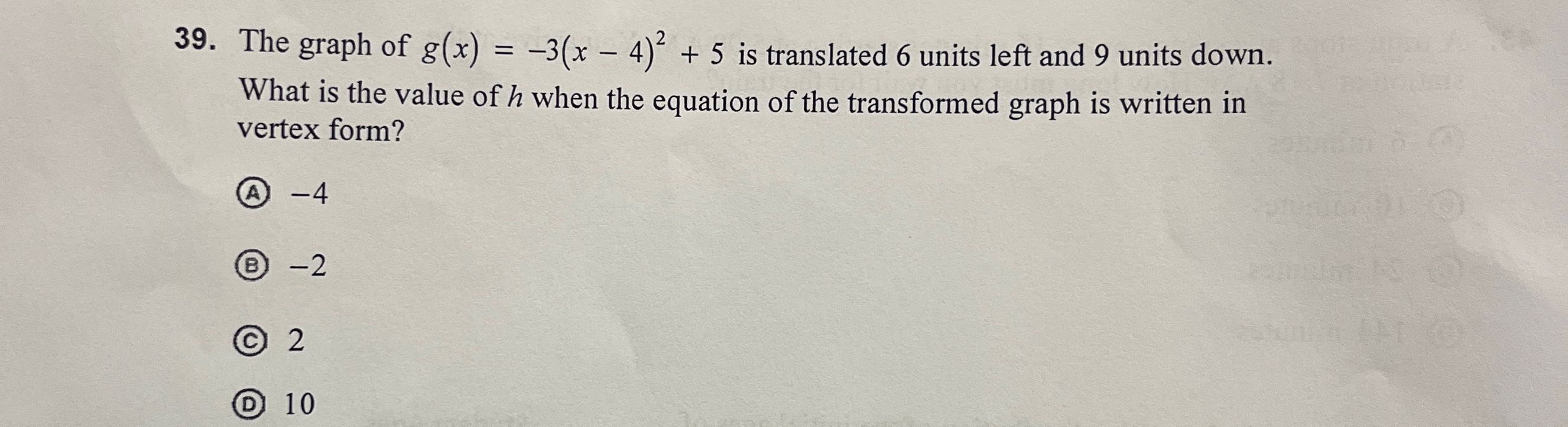Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The graph of
g(x)=-3(x-4)^(2)+5 is translated 6 units left and 9 units down. What is the value of
h when the equation of the transformed graph is written in vertex form?
(A) -4
(B) -2
(C) 2
(D) 10

$39$ . The graph of $g(x)=-3(x-4)^{2}+5$ is translated $6$ units left and $9$ units down. What is the value of $h$ when the equation of the transformed graph is written in vertex form? $\newline$ (A) $-4$ $\newline$ (B) $-2$ $\newline$ (C) $2$ $\newline$ (D) $10$

View step-by-step help

View step-by-step help

Convert equations of parabolas from general to vertex form

Full solution

Q.

39

. The graph of

g(x)=-3(x-4)^{2}+5

is translated

6

units left and

9

units down. What is the value of

h

when the equation of the transformed graph is written in vertex form?

\newline

(A)

-4

\newline

(B)

-2

\newline

(C)

2

\newline

(D)

10

Identify Vertex Form and Vertex: Identify the original vertex form and the vertex of $g(x)$ . $\newline$ Original vertex form: $g(x) = -3(x - 4)^2 + 5$ $\newline$ Vertex: $(4, 5)$
Apply Translation to Vertex: Apply the translation to the vertex. $\newline$ Translation: $6$ units left and $9$ units down. $\newline$ New vertex: $(4 - 6, 5 - 9) = (-2, -4)$
Write New Vertex Form: Write the new vertex form using the new vertex. $\newline$ New vertex form: $g(x) = -3(x - (-2))^2 - 4$ $\newline$ Simplified: $g(x) = -3(x + 2)^2 - 4$
Identify Value of h: Identify the value of h from the new vertex form. $\newline$ From $g(x) = -3(x + h)^2 + k$ , $h = 2$

More problems from Convert equations of parabolas from general to vertex form

Question

What is the focus of the parabola

y = -x^2

\newline

Simplify any fractions.

\newline

(_____ , _____)

\newline

Posted 2 months ago

Question

The equation of a parabola is

y = x^2 - 10x + 25

. Write the equation in vertex form.

\newline

Write any numbers as integers or simplified proper or improper fractions.

\newline

Posted 3 months ago

Question

In which direction does the parabola

x + y^2 = -7

\newline

\newline

\text{up}

\newline

\text{down}

\newline

\text{right}

\newline

\text{left}

Posted 3 months ago

Question

What is the vertex of the parabola

y = -4(x - 2)^2 + 2

?

\newline

(\_,\_)

Posted 3 months ago

Question

What is the axis of symmetry of the parabola

x = \frac{1}{2}(y + 3)^2 + 5

Posted 3 months ago

Question

In which direction does the parabola

x - 2y^2 = -5

\newline

\newline

\text{[A]up}

\newline

\text{[B]down}

\newline

\text{[C]right}

\newline

\text{[D]left}

Posted 3 months ago

Question

What is the vertex of the parabola

y - 8x^2 = 4

\newline

(\_,\_)

Posted 2 months ago

Question

The equation of a circle is

x^{2}+(y+4)^{2}=1

. What are the center and radius of the circle?

\newline

1

\newline

(A) The center is

(-4,0)

and the radius is

1

\newline

(B) The center is

(4,0)

and the radius is

1

\newline

(C) The center is

(0,4)

and the radius is

1

\newline

(D) The center is

(0,-4)

and the radius is

1

Posted 4 months ago

Question

y=(x-3)(x+9)

\newline

The given equation is graphed in the

x y

-plane. Which of the following are

x

-intercepts of the graph?

\newline

1

\newline

-3

-9

\newline

-3

9

\newline

3

-9

\newline

3

9

Posted 4 months ago

Question

y=2 x^{2}-5 x+7

is graphed in the

x y

-plane, which of the following characteristics of the graph is displayed as a constant or coefficient in the equation?

\newline

1

\newline

x

\newline

y

\newline

x

-coordinate of the vertex

\newline

y

-coordinate of the vertex

Posted 4 months ago