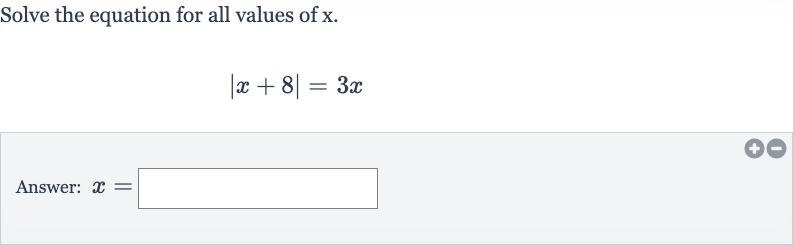Solve the equation for all values of x. |x+8|=3x Answer: x=

Question

Solve the equation for all values of  x.  |x+8|=3x Answer:  x=

Bytelearn · Accepted Answer

Absolute Value Equation Split: We have the equation |x+8|=3x. The absolute value equation can split into two separate equations, one for the positive case and one for the negative case. For the positive case, we have: x + 8 = 3xPositive Case Solution: To solve for x, we need to get all the x terms on one side. Subtract x from both sides of the equation: x + 8 - x = 3x - x 8 = 2xNegative Case Solution: Now, divide both sides by 2 to solve for x: 8 / 2 = 2x / 2 4 = xPositive Case Simplification: For the negative case, we have: -(x + 8) = 3x -x - 8 = 3xPositive Case Solution: To solve for x, we need to get all the x terms on one side. Add x to both sides of the equation: -x - 8 + x = 3x + x -8 = 4xNegative Case Simplification: Now, divide both sides by 4 to solve for x: -8 / 4 = 4x / 4 -2 = xNegative Case Solution: We have found two potential solutions for the equation |x+8|=3x: x = 4 and x = -2. However, we must check these solutions to ensure they do not violate the original absolute value equation.Check x = 4: Check x = 4 in the original equation: |4 + 8| = 3 * 4 |12| = 12 12 = 12 which is true.Check x = -2: Check x = -2 in the original equation: |-2 + 8| = 3 * -2 |6| = -6 6 ≠ -6 which is false. Therefore, x = -2 is not a solution.

Solve the equation for all values of $x$ . $\newline$ $|x+8|=3 x$ $\newline$ Answer: $x=$

Full solution

More problems from Evaluate absolute value expressions

Related topics

Solve the equation for all values of x x x.\newline∣x+8∣=3x |x+8|=3 x ∣x+8∣=3x\newlineAnswer: x= x= x=

Solve the equation for all values of $x$ . $\newline$ $|x+8|=3 x$ $\newline$ Answer: $x=$