Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

log_(4)8=

$\log _{4} 8=$

View step-by-step help

View step-by-step help

Relationship between squares and square roots

Full solution

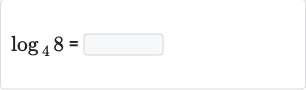
Q.

\log _{4} 8=

Find value of $\log$ : We need to find the value of $\log_{4}8$ . This means we are looking for the exponent that $4$ must be raised to in order to get $8$ .
Express $8$ and $4$ as powers of $2$ : We can express $8$ as $2^3$ and $4$ as $2^2$ . This will allow us to use the property of logarithms that states $\log_{b}(b^x) = x$ .
Rewrite expression with new representations: Rewrite the original expression using the new representations of $8$ and $4$ : $\log_{(2^2)}(2^3)$ .
Apply property of logarithms: Apply the property of logarithms that allows us to divide the exponents when the base of the logarithm and the argument have the same base: $\log_{2^2}(2^3) = \frac{3}{2}$ .
Final value of log: The value of $\log_{4}8$ is therefore $\frac{3}{2}$ . This is the exponent that $4$ (which is $2^{2}$ ) must be raised to in order to get $8$ .

More problems from Relationship between squares and square roots

Question

Solve the following equation for

y

\newline

\begin{array}{l} y+6=\sqrt{2 y^{2}+72} \\ y=\square \end{array}

Posted 4 months ago

Question

z=12.1+29 i

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 4 months ago

Question

z=-400 i-44.5

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 4 months ago

Question

z=-91+14.6 i

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 4 months ago

Question

z=44 i+23.3

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 4 months ago

Question

\log _{16} 8=

Posted 4 months ago

Question

\log _{5} 25=

Posted 4 months ago

Question

\log _{49} 7=

Posted 4 months ago

Question

\log _{3} 27=

Posted 4 months ago

Question

\log _{7} 49=

Posted 4 months ago