Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

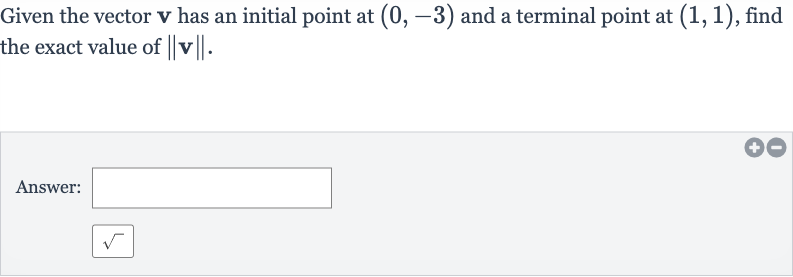
Given the vector
v has an initial point at
(0,-3) and a terminal point at
(1,1), find the exact value of
||v||.
Answer:

Given the vector $\mathbf{v}$ has an initial point at $(0,-3)$ and a terminal point at $(1,1)$ , find the exact value of $\|\mathbf{v}\|$ . $\newline$ Answer:

View step-by-step help

View step-by-step help

Transformations of absolute value functions: translations and reflections

Full solution

Q. Given the vector

\mathbf{v}

has an initial point at

(0,-3)

and a terminal point at

(1,1)

, find the exact value of

\|\mathbf{v}\|

.

\newline

Answer:

Define Initial and Terminal Points: To find the magnitude of vector $v$ , we need to calculate the difference in the $x$ -coordinates and the difference in the $y$ -coordinates between the terminal point and the initial point. Then, we will use the Pythagorean theorem to find the magnitude. $\newline$ Let's denote the initial point as $(x_1, y_1) = (0, -3)$ and the terminal point as $(x_2, y_2) = (1, 1)$ .
Calculate Differences: Calculate the difference in the x-coordinates ( $\Delta x$ ) and the difference in the y-coordinates ( $\Delta y$ ). $\newline$ $\Delta x = x_2 - x_1 = 1 - 0 = 1$ $\newline$ $\Delta y = y_2 - y_1 = 1 - (-3) = 1 + 3 = 4$
Use Pythagorean Theorem: Now, we use the Pythagorean theorem to find the magnitude of vector $v$ , which is denoted as $||v||$ . $||v|| = \sqrt{(\Delta x^2 + \Delta y^2)} = \sqrt{(1^2 + 4^2)} = \sqrt{(1 + 16)} = \sqrt{17}$

More problems from Transformations of absolute value functions: translations and reflections

Question

\begin{array}{l}z=-24 i-19 \\ \operatorname{Re}(z)= \\ \operatorname{Im}(z)=\end{array}

Posted 4 months ago

Question

\begin{array}{l}z=-13-52 i \\ \operatorname{Re}(z)= \\ \operatorname{Im}(z)=\end{array}

Posted 4 months ago

Question

What happens to the value of the expression

\frac{10}{d}

d

increases from a small positive number to a large positive number?

\newline

1

\newline

(A) It increases.

\newline

(B) It decreases.

\newline

(C) It stays the same.

Posted 4 months ago

Question

What happens to the value of the expression

\frac{5}{x}+5

x

decreases from a large positive number to a small positive number?

\newline

1

\newline

(A) It increases.

\newline

(B) It decreases.

\newline

(C) It stays the same.

Posted 4 months ago

Question

What happens to the value of the expression

c+2

c

\newline

1

\newline

(A) It increases.

\newline

(B) It decreases.

\newline

(C) It stays the same.

Posted 4 months ago

Question

What happens to the value of the expression

\frac{50}{p}

p

decreases from a large positive number to a small positive number?

\newline

1

\newline

(A) It increases.

\newline

(B) It decreases.

\newline

(C) It stays the same.

Posted 4 months ago

Question

What happens to the value of the expression

b-1

b

\newline

1

\newline

(A) It increases.

\newline

(B) It decreases.

\newline

(C) It stays the same.

Posted 4 months ago

Question

What happens to the value of the expression

\frac{q}{20}

q

\newline

1

\newline

(A) It increases.

\newline

(B) It decreases.

\newline

(C) It stays the same.

Posted 4 months ago

Question

Given the vector

\mathbf{v}

has an initial point at

(-1,3)

and a terminal point at

(-2,4)

, find the exact value of

\|\mathbf{v}\|

\newline

Posted 2 months ago

Question

Given the vector

\mathbf{v}

has an initial point at

(7,6)

and a terminal point at

(1,0)

, find the exact value of

\|\mathbf{v}\|

\newline

Posted 2 months ago