AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
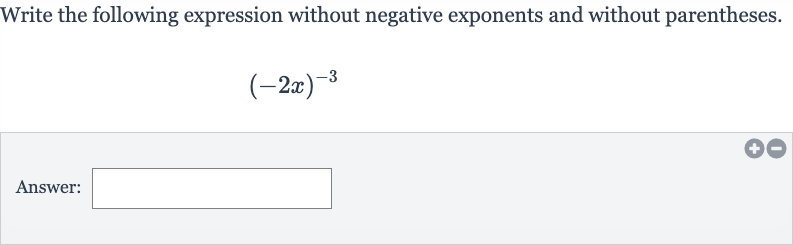
Write the following expression without negative exponents and without parentheses.Answer:
Full solution
Q. Write the following expression without negative exponents and without parentheses.Answer:
- Understand Negative Exponents: First, we need to understand the properties of negative exponents. The negative exponent indicates that we should take the reciprocal of the base. So, means we should take the reciprocal of and then raise it to the power of .
- Reciprocal and Cubing: Taking the reciprocal of gives us . Now we need to raise this to the power of , which means we will cube both the numerator and the denominator.
- Simplify the Expression: Cubing the numerator gives us . Cubing the denominator gives us because is and is .
- Simplify the Expression: Cubing the numerator gives us . Cubing the denominator gives us because is and is .Putting it all together, we have which simplifies to . Since we typically don't leave negative signs in the denominator, we can write this as .
