Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which of the following is equivalent to
sec ((2pi)/(7)) ?

sec ((9pi)/(7))

sec ((19 pi)/(7))

sec ((12 pi)/(7))

sec ((5pi)/(7))

Which of the following is equivalent to $\sec \frac{2 \pi}{7}$ ? $\newline$ $\sec \frac{9 \pi}{7}$ $\newline$ $\sec \frac{19 \pi}{7}$ $\newline$ $\sec \frac{12 \pi}{7}$ $\newline$ $\sec \frac{5 \pi}{7}$

View step-by-step help

View step-by-step help

Write a formula for an arithmetic sequence

Full solution

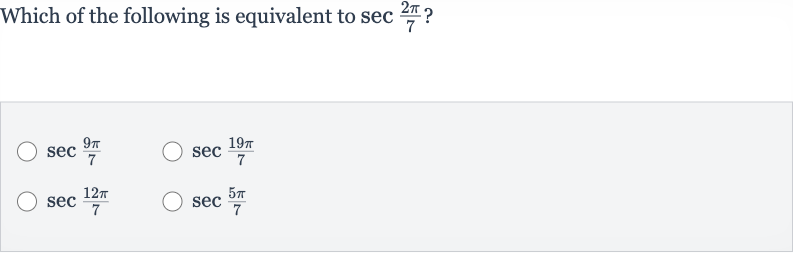
Q. Which of the following is equivalent to

\sec \frac{2 \pi}{7}

?

\newline

\sec \frac{9 \pi}{7}

\newline

\sec \frac{19 \pi}{7}

\newline

\sec \frac{12 \pi}{7}

\newline

\sec \frac{5 \pi}{7}

Understand Secant Function Properties: Understand the properties of the secant function. The secant function, $\sec(\theta)$ , is periodic with a period of $2\pi$ . This means that $\sec(\theta) = \sec(\theta + 2\pi k)$ for any integer $k$ . We will use this property to find an equivalent expression for $\sec(\frac{2\pi}{7})$ .
Compare with Options: Compare the given options with the original expression $\sec\left(\frac{2\pi}{7}\right)$ by adding multiples of $2\pi$ to the original angle and see which option matches. We will start with $\sec\left(\frac{9\pi}{7}\right)$ and check if it is equivalent to $\sec\left(\frac{2\pi}{7}\right)$ .
Check $\sec\left(\frac{9\pi}{7}\right)$ : Add $2\pi$ to the original angle $\frac{2\pi}{7}$ to see if it matches $\sec\left(\frac{9\pi}{7}\right)$ . The calculation is $\frac{2\pi}{7} + 2\pi = \frac{2\pi + 14\pi}{7} = \frac{16\pi}{7}$ . This does not match $\sec\left(\frac{9\pi}{7}\right)$ , so $\sec\left(\frac{9\pi}{7}\right)$ is not equivalent to $\sec\left(\frac{2\pi}{7}\right)$ .
Check $\sec\left(\frac{19\pi}{7}\right)$ : Check $\sec\left(\frac{19\pi}{7}\right)$ by adding $2\pi$ to the angle $\frac{2\pi}{7}$ twice. The calculation is $\frac{2\pi}{7} + 2\times2\pi = \frac{2\pi}{7} + \frac{28\pi}{7} = \frac{30\pi}{7}$ . This simplifies to $\frac{2\times14\pi + 2\pi}{7} = \frac{28\pi + 2\pi}{7} = \frac{30\pi}{7}$ . This does not match $\sec\left(\frac{19\pi}{7}\right)$ , so $\sec\left(\frac{19\pi}{7}\right)$ is not equivalent to $\sec\left(\frac{2\pi}{7}\right)$ .
Check $\sec\left(\frac{12\pi}{7}\right)$ : Check $\sec\left(\frac{12\pi}{7}\right)$ by subtracting $2\pi$ from the angle $\frac{2\pi}{7}$ . The calculation is $\frac{2\pi}{7} - 2\pi = \frac{2\pi - 14\pi}{7} = \frac{-12\pi}{7}$ . This does not match $\sec\left(\frac{12\pi}{7}\right)$ , so $\sec\left(\frac{12\pi}{7}\right)$ is not equivalent to $\sec\left(\frac{2\pi}{7}\right)$ .
Check $\sec\left(\frac{5\pi}{7}\right)$ : Check $\sec\left(\frac{5\pi}{7}\right)$ by adding $2\pi$ to the angle $\frac{2\pi}{7}$ three times. The calculation is $\frac{2\pi}{7} + 3\times2\pi = \frac{2\pi}{7} + \frac{42\pi}{7} = \frac{44\pi}{7}$ . This simplifies to $\frac{6\times7\pi + 2\pi}{7} = \frac{42\pi + 2\pi}{7} = \frac{44\pi}{7}$ . This does not match $\sec\left(\frac{5\pi}{7}\right)$ , so $\sec\left(\frac{5\pi}{7}\right)$ is not equivalent to $\sec\left(\frac{2\pi}{7}\right)$ .
Correct Approach for Finding $k$ : Realize that there was a mistake in the previous steps. We need to find a $k$ such that $\frac{2\pi}{7} + 2\pi k =$ one of the given options. We should have been looking for a $k$ that makes the expression $\frac{2\pi}{7} + \frac{2\pi k}{7} =$ one of the given options. We will re-evaluate the options with this corrected approach.

More problems from Write a formula for an arithmetic sequence

Question

Find the sum of the finite arithmetic series.

\sum_{n=1}^{10} (7n+4)

\newline

Posted 3 months ago

Question

Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`

Posted 2 months ago

Question

Type the missing number in this sequence: `2, 4 8`, ______,`32`

Posted 2 months ago

Question

What kind of sequence is this?

2, 10, 50, 250, \ldots

Choices:Choices:

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 2 months ago

Question

What is the missing number in this pattern?

1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_

Posted 2 months ago

Question

Classify the series.

\sum_{n = 0}^{12} (n + 2)^3

\newline

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 2 months ago

Question

Find the first three partial sums of the series.

\newline

1 + 6 + 11 + 16 + 21 + 26 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 2 months ago

Question

Find the third partial sum of the series.

\newline

3 + 9 + 15 + 21 + 27 + 33 + \cdots

\newline

Write your answer as an integer or a fraction in simplest form.

\newline

S_3 =

Posted 2 months ago

Question

Find the first three partial sums of the series.

\newline

1 + 7 + 13 + 19 + 25 + 31 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 3 months ago

Question

Does the infinite geometric series converge or diverge?

\newline

1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots

\newline

\newline

\text{[A]converge}

\newline

\text{[B]diverge}

Posted 2 months ago