Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is the volume of a hemisphere with a diameter of
57.6m, rounded to the nearest tenth of a cubic meter?
Answer:
m^(3)

What is the volume of a hemisphere with a diameter of $57.6 \mathrm{~m}$ , rounded to the nearest tenth of a cubic meter? $\newline$ Answer: $\mathrm{m}^{3}$

View step-by-step help

View step-by-step help

Convert between customary and metric systems

Full solution

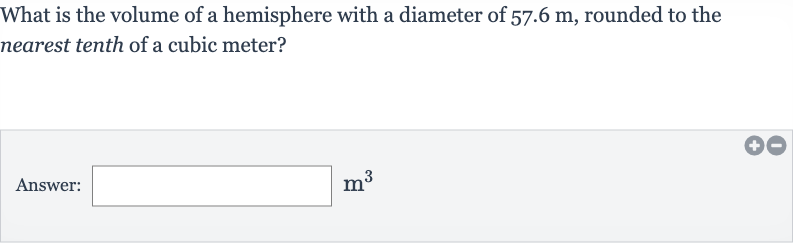
Q. What is the volume of a hemisphere with a diameter of

57.6 \mathrm{~m}

, rounded to the nearest tenth of a cubic meter?

\newline

Answer:

\mathrm{m}^{3}

Calculate Radius: To find the volume of a hemisphere, we first need to find the volume of a full sphere and then divide it by $2$ . The formula for the volume of a sphere is $V = \frac{4}{3}\pi r^3$ , where $r$ is the radius of the sphere. Since the diameter of the sphere is given as $57.6$ meters, the radius $r$ is half of the diameter. $\newline$ Calculation: $r = \frac{\text{diameter}}{2} = \frac{57.6\text{m}}{2} = 28.8\text{m}$
Substitute Radius in Formula: Now we can substitute the radius into the formula for the volume of a sphere. $\newline$ Calculation: $V_{\text{sphere}} = \frac{4}{3}\pi(28.8\,\text{m})^3$
Calculate Volume of Full Sphere: We calculate the volume of the full sphere using the radius we found. $\newline$ Calculation: $V_{\text{sphere}} = \frac{4}{3}\pi(28.8\,\text{m})^3 = \frac{4}{3}\pi(23832.832\,\text{m}^3) \approx \frac{4}{3} \times 3.14159 \times 23832.832\,\text{m}^3 \approx 125663.706\,\text{m}^3$
Divide Volume by $2$ : Since we want the volume of a hemisphere, we divide the volume of the sphere by $2$ . $\newline$ Calculation: $V_{\text{hemisphere}} = \frac{V_{\text{sphere}}}{2} \approx \frac{125663.706\,\text{m}^3}{2} \approx 62831.853\,\text{m}^3$
Round Final Volume: Finally, we round the volume of the hemisphere to the nearest tenth of a cubic meter. $\newline$ Calculation: $V_{\text{hemisphere}} \approx 62831.9\,\text{m}^3$

More problems from Convert between customary and metric systems

Question

\newline

1

2

\_\_\_\_\_

Posted 2 months ago

Question

710

milliliters of energy drink yesterday. How many liters of energy drink did he consume?

\newline

(Round your answer to the nearest hundredth of a liter.)

Posted 2 months ago

Question

A real estate purveyor purchases a

60

000

\left(\mathrm{ft}^{2}\right)

warehouse and decides to turn it into a storage facility. The warehouse's width is exactly

\frac{2}{3}

of its length. What is the warehouse's width? Round your answer to the nearest foot.

Posted 2 months ago

Question

3

cups (c) of flour to bake

2

loaves of bread. If

1

pound (lb) of flour is equivalent to

3 \frac{1}{3} \mathrm{c}

, how many loaves of bread can the baker make with a

10 \mathrm{lb}

\newline

(Round the answer to the nearest whole number.)

Posted 1 month ago

Question

\$ 2500

into a savings account.

\newline

The relationship between the time,

t

, in years, since the account was first opened, and Ella's account balance,

B(t)

, in dollars, is modeled by the following function.

\newline

B(t)=2500 \cdot e^{0.025 t}

\newline

What will the balance of Ella's savings account be after

4

years? Round your answer, if necessary, to the nearest hundredth.

\newline

\$

Posted 2 months ago

Question

Maya needs to rent a car while on vacation. The rental company charges

\$17.95

18

cents for each mile driven. If Maya only has

\$40

to spend on the car rental, what is the maximum number of miles she can drive?

\newline

\newline

(Round your answer down to the nearest whole mile)

Posted 3 months ago

Question

What is the area of a circle whose circumference is

1447

\pi=3.14

166698.73\,\text{m}^2

Posted 3 months ago

Question

What is the area of a circle whose circumference is

1447

\pi = 3.14

166698.73 \, \text{m}^2

Posted 2 months ago

Question

13

feet to meters using

3.281

1

\newline

Round answers to hundredths of meters (or

2

decimal places)

Posted 3 months ago

Question

14

feet to meters using

3.281

1

\newline

Round answers to hundredths of meters (or

2

decimal places)

Posted 3 months ago