AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
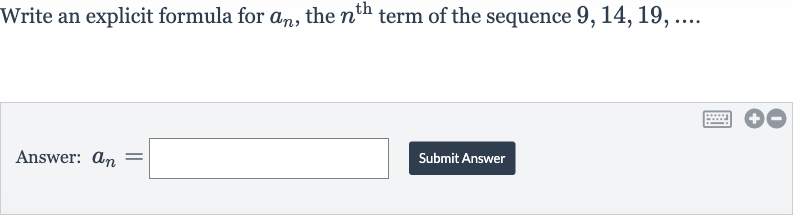
Write an explicit formula for , the term of the sequence Answer:
Full solution
Q. Write an explicit formula for , the term of the sequence Answer:
- Determine Common Difference: To find the explicit formula for the th term of the sequence, we first need to determine the common difference between consecutive terms.
- Calculate Common Difference: We subtract the first term from the second term to find the common difference.
- Identify Arithmetic Sequence: The common difference is . This means that each term is more than the previous term. The sequence is an arithmetic sequence.
- Arithmetic Sequence Formula: The explicit formula for an arithmetic sequence is given by:where is the first term and is the common difference.
- Substitute Values: We know that and . Let's substitute these values into the formula.
- Distribute and Simplify: Simplify the formula by distributing the into the parentheses.
- Combine Like Terms: Combine like terms to get the final explicit formula.
