AI tutor
Full solution
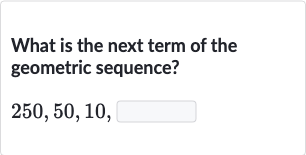
Q. What is the next term of the geometric sequence?,
- Identify sequence type: Identify the type of sequence.The sequence decreases by a constant factor each time. This indicates that it is a geometric sequence.
- Determine common ratio: Determine the common ratio of the geometric sequence.To find the common ratio, divide the second term by the first term: .
- Find next term: Use the common ratio to find the next term.The third term is , so to find the fourth term, multiply the third term by the common ratio: .