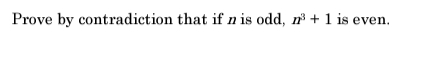Full solution

Q. Prove by contradiction that if

n

is odd,

n^{3}+1

is even.

Assume $n$ is odd: Assume for the sake of contradiction that $n$ is odd and $n^3 + 1$ is not even, which means $n^3 + 1$ is odd.
Express $n$ as $2k + 1$ : An odd number can be expressed in the form of $2k + 1$ , where $k$ is an integer. Since $n$ is odd, let $n = 2k + 1$ .
Substitute $n$ in expression: Substitute $n$ with $2k + 1$ in the expression $n^3 + 1$ to find its value in terms of $k$ . $\newline$ $n^3 + 1 = (2k + 1)^3 + 1$
Expand $(2k + 1)^3$ : Expand the cube $(2k + 1)^3$ using the binomial theorem or by multiplying $(2k + 1)(2k + 1)(2k + 1)$ . $(2k + 1)^3 = 2k(2k(2k + 1) + 1) + 1 = 8k^3 + 12k^2 + 6k + 1$
Add $1$ to get $n^3 + 1$ : Add $1$ to the expanded form of $(2k + 1)^3$ to get $n^3 + 1$ . $\newline$ $n^3 + 1 = 8k^3 + 12k^2 + 6k + 1 + 1 = 8k^3 + 12k^2 + 6k + 2$
Identify even components: Notice that $8k^3$ , $12k^2$ , and $6k$ are all multiples of $2$ , which means they are even. Adding even numbers together will result in an even number. Adding $2$ to an even number will still result in an even number.
Contradiction of initial assumption: Since $n^3 + 1 = 8k^3 + 12k^2 + 6k + 2$ is even, our initial assumption that $n^3 + 1$ is odd leads to a contradiction.
Conclusion by contradiction: Therefore, by contradiction, if $n$ is odd, then $n^3 + 1$ must be even.