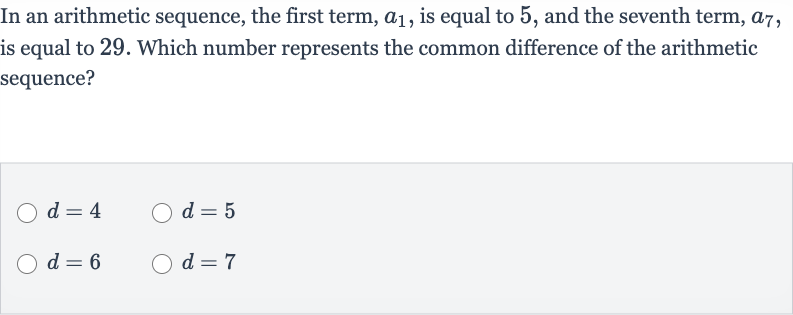Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

In an arithmetic sequence, the first term, a_(1), is equal to 5 , and the seventh term, a_(7), is equal to 29 . Which number represents the common difference of the arithmetic sequence? d=4 d=5 d=6 d=7

In an arithmetic sequence, the first term, a1 a_{1} , is equal to 55 , and the seventh term, a7 a_{7} , is equal to 2929 . Which number represents the common difference of the arithmetic sequence?\newlined=4 d=4 \newlined=5 d=5 \newlined=6 d=6 \newlined=7 d=7

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Convert a recursive formula to an explicit formularight chevron icon

Full solution

Q. In an arithmetic sequence, the first term, a1 a_{1} , is equal to 55 , and the seventh term, a7 a_{7} , is equal to 2929 . Which number represents the common difference of the arithmetic sequence?\newlined=4 d=4 \newlined=5 d=5 \newlined=6 d=6 \newlined=7 d=7
  1. Given terms: We are given the first term of an arithmetic sequence a1=5a_{1} = 5 and the seventh term a7=29a_{7} = 29. We need to find the common difference dd. The formula for the nth term of an arithmetic sequence is an=a1+(n−1)da_{n} = a_{1} + (n - 1)d.
  2. Express seventh term: We can use the formula to express the seventh term in terms of the first term and the common difference: a7=a1+6da_{7} = a_{1} + 6d.
  3. Substitute values: Substitute the given values into the equation: 29=5+6d29 = 5 + 6d.
  4. Solve for d: Now, solve for d: 29−5=6d29 - 5 = 6d.
  5. Simplify equation: Simplify the equation: 24=6d24 = 6d.
  6. Divide by 66: Divide both sides by 66 to find dd: d=246d = \frac{24}{6}.
  7. Calculate d: Calculate the value of d: d=4d = 4.

More problems from Convert a recursive formula to an explicit formula

Question
Find the sum of the finite arithmetic series. ∑n=110(7n+4)\sum_{n=1}^{10} (7n+4)\newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`
Get tutor helpright-arrow

Posted 2 months ago

Question
Type the missing number in this sequence: `2, 4 8`, ______,`32`
Get tutor helpright-arrow

Posted 2 months ago

Question
What kind of sequence is this? 2,10,50,250,…2, 10, 50, 250, \ldots Choices:Choices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the missing number in this pattern? 1,4,9,16,25,36,49,64,81,____1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
Classify the series. ∑n=012(n+2)3 \sum_{n = 0}^{12} (n + 2)^3 \newlineChoices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the first three partial sums of the series.\newline1+6+11+16+21+26+⋯1 + 6 + 11 + 16 + 21 + 26 + \cdots\newlineWrite your answers as integers or fractions in simplest form.\newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the third partial sum of the series. \newline3+9+15+21+27+33+⋯3 + 9 + 15 + 21 + 27 + 33 + \cdots\newlineWrite your answer as an integer or a fraction in simplest form. \newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the first three partial sums of the series. \newline1+7+13+19+25+31+⋯1 + 7 + 13 + 19 + 25 + 31 + \cdots\newlineWrite your answers as integers or fractions in simplest form. \newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 3 months ago

Question
Does the infinite geometric series converge or diverge?\newline1+34+916+2764+⋯1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots\newlineChoices:\newline[A]converge\text{[A]converge}\newline[B]diverge\text{[B]diverge}
Get tutor helpright-arrow

Posted 2 months ago

View all (19)