If $-4-y+x^{2}=y^{2}+3 y^{3}$ then find $\frac{d y}{d x}$ at the point $(-3,1)$ . $\newline$ Answer: $\left.\frac{d y}{d x}\right|_{(-3,1)}=$

View step-by-step help

Home

Math Problems

Algebra 2

Transformations of absolute value functions

Full solution

Q. If

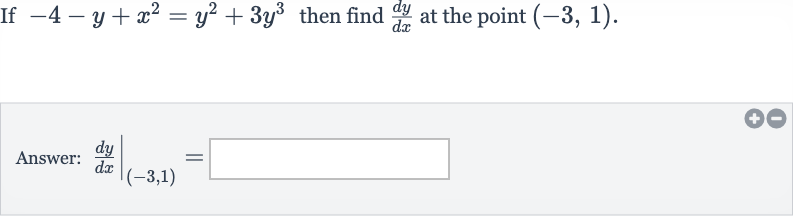
-4-y+x^{2}=y^{2}+3 y^{3}

then find

\frac{d y}{d x}

at the point

(-3,1)

\newline

Answer:

\left.\frac{d y}{d x}\right|_{(-3,1)}=

Differentiate with respect to $x$ : First, we need to differentiate both sides of the equation with respect to $x$ to find $\frac{dy}{dx}$ . The equation is $-4 - y + x^2 = y^2 + 3y^3$ . Differentiating both sides with respect to $x$ gives us: $\frac{d}{dx}(-4 - y + x^2) = \frac{d}{dx}(y^2 + 3y^3)$ .
Apply chain rule: On the left side, the derivative of $-4$ with respect to $x$ is $0$ , the derivative of $-y$ with respect to $x$ is $-\frac{dy}{dx}$ (since $y$ is a function of $x$ ), and the derivative of $x^2$ with respect to $x$ is $x$ $0$ . So, we have: $x$ $1$ .
Collect terms and solve: On the right side, we use the chain rule to differentiate $y^2$ and $3y^3$ with respect to $x$ . The derivative of $y^2$ with respect to $x$ is $2y(\frac{dy}{dx})$ , and the derivative of $3y^3$ with respect to $x$ is $9y^2(\frac{dy}{dx})$ . So, we have: $-\frac{dy}{dx} + 2x = 2y(\frac{dy}{dx}) + 9y^2(\frac{dy}{dx})$ .
Factor out dy/dx: Now, we collect all the terms involving $dy/dx$ on one side of the equation to solve for $dy/dx$ . This gives us: $- dy/dx - 2y(dy/dx) - 9y^2(dy/dx) = 2x$ .
Solve for $\frac{dy}{dx}$ : Factor out $\frac{dy}{dx}$ from the left side of the equation: $\newline$ $\frac{dy}{dx}(-1 - 2y - 9y^2) = 2x$ .
Evaluate at $(-3,1)$ : Now, we can solve for $\frac{dy}{dx}$ by dividing both sides by $(-1 - 2y - 9y^2)$ : $\newline$ $\frac{dy}{dx} = \frac{2x}{-1 - 2y - 9y^2}.$
Perform calculations: We need to evaluate $\frac{dy}{dx}$ at the point $(-3,1)$ . Substitute $x = -3$ and $y = 1$ into the equation: $\newline$ $\frac{dy}{dx}\bigg|_{(-3,1)} = \frac{2(-3)}{(-1 - 2(1) - 9(1)^2)}$ .
Simplify the denominator: Now, perform the calculations: $\newline$ $\frac{dy}{dx}\bigg|_{(-3,1)} = \frac{-6}{(-1 - 2 - 9)}.$
Divide to find value: Simplify the denominator: $\frac{dy}{dx}\bigg|_{(-3,1)} = \frac{-6}{-12}$ .
Divide to find value: Simplify the denominator: $\frac{dy}{dx}\bigg|_{(-3,1)} = \frac{-6}{-12}$ .Finally, divide $-6$ by $-12$ to get the value of $\frac{dy}{dx}$ at the point $(-3,1)$ : $\frac{dy}{dx}\bigg|_{(-3,1)} = \frac{1}{2}$ .