Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the numerical answer to the summation given below.

sum_(n=0)^(92)(6n+3)
Answer:

Find the numerical answer to the summation given below. $\newline$ $\sum_{n=0}^{92}(6 n+3)$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Find the roots of factored polynomials

Full solution

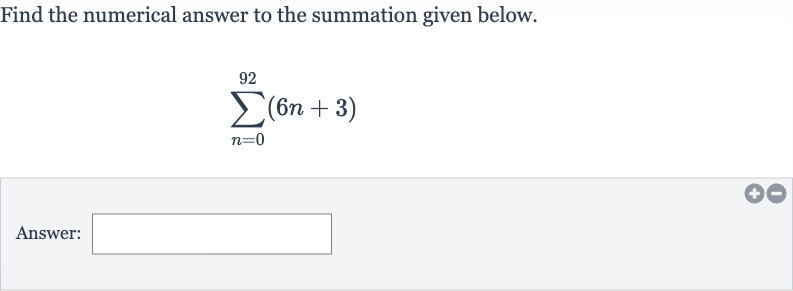
Q. Find the numerical answer to the summation given below.

\newline

\sum_{n=0}^{92}(6 n+3)

\newline

Answer:

Recognize arithmetic series: To solve the summation, we need to recognize that it is the sum of an arithmetic series. The general formula for the sum of an arithmetic series is $S = \frac{n}{2}(a_1 + a_n)$ , where $n$ is the number of terms, $a_1$ is the first term, and $a_n$ is the last term. First, we need to find the number of terms in the series.
Find number of terms: The series starts at $n=0$ and ends at $n=92$ , so the number of terms is $92 - 0 + 1 = 93$ terms.
Find first term: Next, we need to find the first term of the series when $n=0$ . Plugging $n=0$ into the formula $6n+3$ gives us the first term: $a_1 = 6(0) + 3 = 3$ .
Find last term: Now, we need to find the last term of the series when $n=92$ . Plugging $n=92$ into the formula $6n+3$ gives us the last term: $a_n = 6(92) + 3 = 552 + 3 = 555$ .
Use sum formula: We can now use the sum formula for an arithmetic series: $S = \frac{n}{2}(a_1 + a_n)$ . Plugging in the values we have: $S = \frac{93}{2}(3 + 555)$ .
Perform calculation: Perform the calculation inside the parentheses first: $3 + 555 = 558$ .
Multiply by number of terms: Now multiply this sum by the number of terms divided by $2$ : $S = (\frac{93}{2}) \times 558$ .
Perform final calculation: Perform the multiplication to find the sum: $S = 46.5 \times 558$ .
Perform final calculation: Perform the multiplication to find the sum: $S = 46.5 \times 558$ .Finally, calculate the product to get the numerical answer: $S = 25947$ .

More problems from Find the roots of factored polynomials

Question

Find the degree of this polynomial.

\newline

`5b^{10} + 3b^3`

\newline

Posted 3 months ago

Question

\newline

(9a + 5) - (2a + 4)

\newline

Posted 3 months ago

Question

Find the product. Simplify your answer.

\newline

-3v^2(v^2 - 9)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

(v - 3)(4v + 1)

\newline

Posted 3 months ago

Question

Find the square. Simplify your answer.

\newline

(3y + 2)^2

\newline

Posted 3 months ago

Question

Divide. If there is a remainder, include it as a simplified fraction.

\newline

(24t^2 + 36t) \div 6t

\newline

Posted 2 months ago

Question

Is the function

q(x) = x^6 - 9

even, odd, or neither?

\newline

\newline

\text{[[even][odd][neither]]}

Posted 3 months ago

Question

Find the product. Simplify your answer.

\newline

-3q^2(-3q^2 + q)

\newline

Posted 3 months ago

Question

Find the product. Simplify your answer.

\newline

(r + 3)(4r + 2)

\newline

Posted 3 months ago

Question

Find the roots of the factored polynomial.

\newline

(x + 7)(x + 4)

\newline

Write your answer as a list of values separated by commas.

\newline

x =

Posted 3 months ago