Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

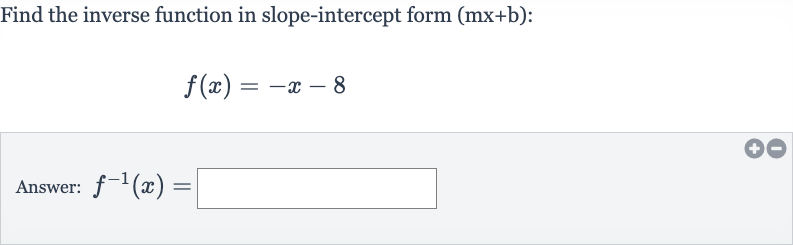
Find the inverse function in slope-intercept form
(mx+b) :

f(x)=-x-8
Answer:
f^(-1)(x)=

Find the inverse function in slope-intercept form $(\mathrm{mx}+\mathrm{b})$ : $\newline$ $f(x)=-x-8$ $\newline$ Answer: $f^{-1}(x)=$

View step-by-step help

View step-by-step help

Find the vertex of the transformed function

Full solution

Q. Find the inverse function in slope-intercept form

(\mathrm{mx}+\mathrm{b})

:

\newline

f(x)=-x-8

\newline

Answer:

f^{-1}(x)=

Write function as $y = -x - 8$ : To find the inverse function, we first write the function as $y = -x - 8$ , where $y$ is the output and $x$ is the input.
Swap roles of x and y: Next, we swap the roles of x and y to find the inverse. This means we replace every $x$ with $y$ and every $y$ with $x$ to get $x = -y - 8$ .
Solve for y: Now, we solve for $y$ to get the inverse function in slope-intercept form. We start by adding $y$ to both sides to get $x + 8 = -y$ .
Multiply by $-1$ : Then, we multiply both sides by $-1$ to solve for $y$ , which gives us $-x - 8 = y$ .
Inverse function in slope-intercept form: The inverse function in slope-intercept form is therefore $f^{-1}(x) = -x - 8$ .

More problems from Find the vertex of the transformed function

Question

Solve by completing the square.

\newline

m^2 - 10m - 29 = 0

\newline

Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.

\newline

`m` = ____ or `m` = _____

Posted 2 months ago

Question

g(x)

g(x)

is the translation

5

f(x)=x^2

\newline

Write your answer in the form

a(x–h)^2+k

a

h

k

\newline

g(x)=

Posted 2 months ago

Question

What is the range of this quadratic function?

\newline

y = x^2 - 4x + 4

\newline

\newline

\left\{y \mid y \geq 2\right\}

\newline

\left\{y \mid y \leq 0\right\}

\newline

\left\{y \mid y \geq 0\right\}

\newline

\text{all real numbers}

Posted 2 months ago

Question

Write the equation of the parabola that passes through the points

(1,0)

(2,0)

(3,\text{–}16)

. Write your answer in the form

y = a(x – p)(x – q)

a

p

q

are integers, decimals, or simplified fractions.

\newline

Posted 2 months ago

Question

Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.

\newline

f^2 + 8f + \_\_\_\_\_

Posted 2 months ago

Question

h

\newline

h^2 + 39h = 0

\newline

\newline

Write each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.

\newline

h =

\newline

Posted 2 months ago

Question

Write a quadratic function with zeros

-9

-7

\newline

Write your answer using the variable

x

and in standard form with a leading coefficient of

1

\newline

f(x) = \_\_\_\_\_

Posted 2 months ago

Question

Find the equation of the axis of symmetry for the parabola

y = x^2

\newline

Simplify any numbers and write them as proper fractions, improper fractions, or integers.

\newline

\underline{\hspace{3cm}}

Posted 3 months ago

Question

g(x)

g(x)

is the translation

8

f(x) = x^2

\newline

Write your answer in the form

a(x – h)^2 + k

a

h

k

\newline

g(x) =

\newline

Posted 3 months ago

Question

x

\newline

x^2 = 1

\newline

\newline

Write your answer in simplified, rationalized form.

\newline

x =

x =

\newline

Posted 3 months ago