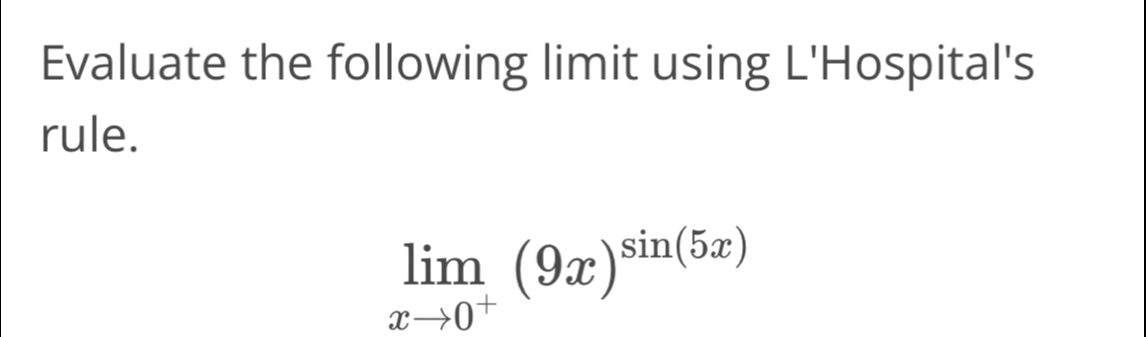Full solution

Q. Evaluate the following limit using L'Hospital's rule.

\newline

\lim _{x \rightarrow 0^{+}}(9 x)^{\sin (5 x)}

Recognize Indeterminate Form: First, recognize that the limit is of the form $0^0$ , which is indeterminate. We can use L'Hospital's Rule by taking the natural log of the function and then exponentiating the result at the end.
Take Natural Log: Let's set $y = (9x)^{(\sin(5x))}$ and take the natural log of both sides to get $\ln(y) = \sin(5x) \cdot \ln(9x)$ .
Find Limit of $\ln(y)$ : Now we find the limit of $\ln(y)$ as $x$ approaches $0$ from the positive side. We have $\lim_{x \to 0^{+}} (\sin(5x) \cdot \ln(9x))$ .
Apply L'Hospital's Rule: We can apply L'Hospital's Rule to this limit since it's in the indeterminate form $0 \cdot (-\infty)$ . Differentiate the numerator and denominator with respect to $x$ .
Differentiate Numerator and Denominator: The derivative of $\sin(5x)$ with respect to $x$ is $5\cos(5x)$ , and the derivative of $\ln(9x)$ with respect to $x$ is $\frac{1}{x}$ .
Simplify the Limit: Now we have $\lim_{x \to 0^{+}} \left(\frac{5\cos(5x)}{1/x}\right)$ . This simplifies to $\lim_{x \to 0^{+}} (5x \cdot \cos(5x))$ .
Evaluate Limit: As $x$ approaches $0$ , $5x$ approaches $0$ and $\cos(5x)$ approaches $1$ . So the limit of $5x \cdot \cos(5x)$ as $x$ approaches $0$ is $0$ .
Exponentiate to Find Limit of $y$ : Since we took the natural log earlier, we need to exponentiate to get the limit of $y$ . So, $e^{0} = 1$ .