Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

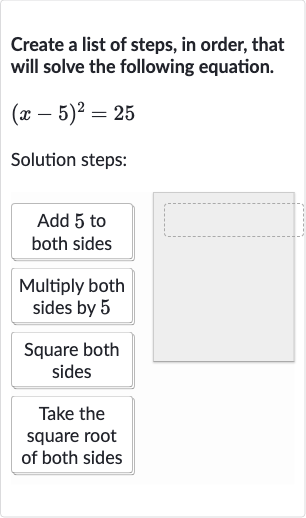
Create a list of steps, in order, that will solve the following equation.

(x-5)^(2)=25
Solution steps:
Add 5 to both sides
Multiply both sides by 5
Square both sides
Take the square root of both sides

Create a list of steps, in order, that will solve the following equation. $\newline$ $(x-5)^{2}=25$ $\newline$ Solution steps: $\newline$ - Add $5$ to both sides $\newline$ - Multiply both sides by $5$ $\newline$ - Square both sides $\newline$ - Take the square root of both sides

View step-by-step help

View step-by-step help

Solve a quadratic equation using square roots

Full solution

Q. Create a list of steps, in order, that will solve the following equation.

\newline

(x-5)^{2}=25

\newline

Solution steps:

\newline

- Add

5

to both sides

\newline

- Multiply both sides by

5

\newline

- Square both sides

\newline

- Take the square root of both sides

Take square root: Take the square root of both sides of the equation to eliminate the exponent on the left side. $\newline$ $\sqrt{((x-5)^2)} = \sqrt{25}$ $\newline$ This simplifies to $|x - 5| = 5$ , because the square root of a square gives the absolute value of the original expression.
Solve absolute value equation: Solve the resulting absolute value equation. The absolute value equation $|x - 5| = 5$ has two possible solutions: $x - 5 = 5$ or $x - 5 = -5$ .
Solve first equation: Solve the first equation $x - 5 = 5$ . $\newline$ Add $5$ to both sides to isolate $x$ . $\newline$ $x - 5 + 5 = 5 + 5$ $\newline$ $x = 10$
Solve second equation: Solve the second equation $x - 5 = -5$ . $\newline$ Add $5$ to both sides to isolate $x$ . $\newline$ $x - 5 + 5 = -5 + 5$ $\newline$ $x = 0$

More problems from Solve a quadratic equation using square roots

Question

Solve by completing the square.

\newline

m^2 - 10m - 29 = 0

\newline

Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.

\newline

`m` = ____ or `m` = _____

Posted 2 months ago

Question

g(x)

g(x)

is the translation

5

f(x)=x^2

\newline

Write your answer in the form

a(x–h)^2+k

a

h

k

\newline

g(x)=

Posted 2 months ago

Question

What is the range of this quadratic function?

\newline

y = x^2 - 4x + 4

\newline

\newline

\left\{y \mid y \geq 2\right\}

\newline

\left\{y \mid y \leq 0\right\}

\newline

\left\{y \mid y \geq 0\right\}

\newline

\text{all real numbers}

Posted 2 months ago

Question

Write the equation of the parabola that passes through the points

(1,0)

(2,0)

(3,\text{–}16)

. Write your answer in the form

y = a(x – p)(x – q)

a

p

q

are integers, decimals, or simplified fractions.

\newline

Posted 2 months ago

Question

Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.

\newline

f^2 + 8f + \_\_\_\_\_

Posted 2 months ago

Question

h

\newline

h^2 + 39h = 0

\newline

\newline

Write each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.

\newline

h =

\newline

Posted 2 months ago

Question

Write a quadratic function with zeros

-9

-7

\newline

Write your answer using the variable

x

and in standard form with a leading coefficient of

1

\newline

f(x) = \_\_\_\_\_

Posted 2 months ago

Question

Find the equation of the axis of symmetry for the parabola

y = x^2

\newline

Simplify any numbers and write them as proper fractions, improper fractions, or integers.

\newline

\underline{\hspace{3cm}}

Posted 3 months ago

Question

g(x)

g(x)

is the translation

8

f(x) = x^2

\newline

Write your answer in the form

a(x – h)^2 + k

a

h

k

\newline

g(x) =

\newline

Posted 3 months ago

Question

x

\newline

x^2 = 1

\newline

\newline

Write your answer in simplified, rationalized form.

\newline

x =

x =

\newline

Posted 3 months ago