AI tutor
Full solution
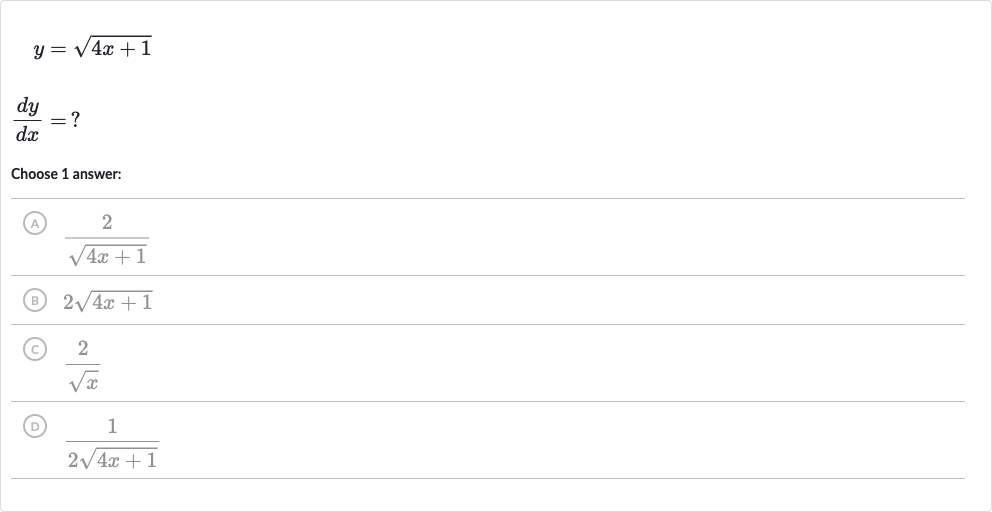
Q. Choose answer:(A) (B) (C) (D)
- Apply Chain Rule: To find the derivative of with respect to , we will use the chain rule. The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function.
- Identify Outer and Inner Functions: The outer function is the square root function, and the inner function is . The derivative of the outer function, , with respect to is . The derivative of the inner function, , with respect to is .
- Calculate Derivative: Applying the chain rule, we multiply the derivative of the outer function by the derivative of the inner function. This gives us .
- Simplify Expression: Simplify the expression by multiplying by , which gives us . So the derivative is .