Full solution
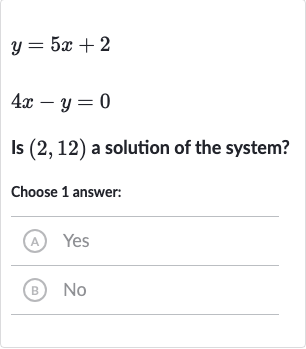
Q. Is a solution of the system?Choose answer:(A) Yes(B) No
- Substitute and Check First Equation: First, we will substitute the point into the first equation and check if it holds true. The first equation is . If we substitute and , we get .
- Verify First Equation: After performing the calculation, we find that , which simplifies to . This is true, so the point satisfies the first equation.
- Substitute and Check Second Equation: Next, we will substitute the point into the second equation and check if it holds true. The second equation is . If we substitute and , we get .
- Verify Second Equation: After performing the calculation, we find that , which is not equal to . Therefore, the point does not satisfy the second equation.
- Solution to the System of Equations: Since the point does not satisfy both equations, it is not a solution to the system of equations.
More problems from Is (x, y) a solution to the system of equations?
QuestionGet tutor help
QuestionGet tutor help