Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which of the following is equivalent to
log_(4)(m)*log_(m)(20) ?
Choose 1 answer:
(A) 5
(B) 80
(c)
log(5)
(D)
log_(4)(20)

Which of the following is equivalent to $\log _{4}(m) \cdot \log _{m}(20)$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $5$ $\newline$ (B) $80$ $\newline$ (C) $\log (5)$ $\newline$ (D) $\log _{4}(20)$

View step-by-step help

View step-by-step help

Product property of logarithms

Full solution

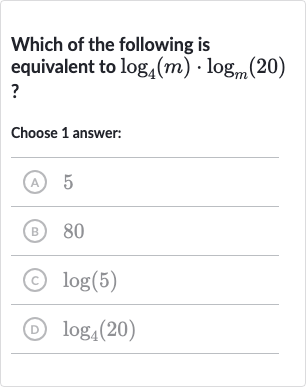
Q. Which of the following is equivalent to

\log _{4}(m) \cdot \log _{m}(20)

?

\newline

Choose

1

answer:

\newline

(A)

5

\newline

(B)

80

\newline

(C)

\log (5)

\newline

(D)

\log _{4}(20)

Use Change of Base Formula: We can use the change of base formula for logarithms, which states that $\log_{a}(b) \cdot \log_{b}(c) = \log_{a}(c)$ . This is because $\log_{a}(b)$ is the exponent to which 'a' must be raised to get 'b', and $\log_{b}(c)$ is the exponent to which 'b' must be raised to get 'c'. When you multiply these, you get the exponent to which 'a' must be raised to get 'c'.
Apply Change of Base Formula: Applying the change of base formula to $\log_{4}(m)\cdot\log_{m}(20)$ , we get: $\newline$ $\log_{4}(m)\cdot\log_{m}(20) = \log_{4}(20)$
Check Answer Choices: Now we need to check the answer choices to see which one matches our result. The correct answer should be $\log_{4}(20)$ .
Identify Correct Answer: Looking at the answer choices, we see that (D) $\log_{4}(20)$ is the correct match for our result.

More problems from Product property of logarithms

Question

Write the exponential equation in logarithmic form.

\newline

9^3 = 729

\newline

\log_\square 729 = 3

Posted 3 months ago

Question

Write the exponential equation in logarithmic form.

\newline

e^4 \approx 54.598

\newline

\ln\_\_\_\_ \approx 4

Posted 3 months ago

Question

Write the logarithmic equation in exponential form.

\newline

\log_{10}100 = 2

\newline

10^2 = \underline{\hspace{2em}}

Posted 3 months ago

Question

Evaluate. Write your answer as a whole number, proper fraction, or improper fraction in simplest form.

\newline

\frac{\ln (e)}{10} =

Posted 3 months ago

Question

Rewrite as a quotient of two common logarithms. Write your answer in simplest form.

\newline

\log_3 33 =

Posted 3 months ago

Question

Evaluate. Round your answer to the nearest thousandth.

\newline

\log_{5}50 =

Posted 3 months ago

Question

Which property of logarithms does this equation demonstrate?

\newline

\log_3 3 + \log_3 6 = \log_3 18

\newline

\newline

\text{Product Property}

\newline

\text{Power Property}

\newline

\text{Quotient Property}

Posted 3 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log(uv)

\newline

Posted 3 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log v^7

\newline

Posted 3 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of base-

6

logarithms or multiples of base-

6

logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log_6 w^6

\newline

Posted 3 months ago