Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which exponential expression is equivalent to
root(7)(b) ?
Choose 1 answer:
(A)
b^(7)
(B)
b^((1)/(7))
(C)
(1)/(b^(7))
(D)
(1)/(b^((1)/(7)))

Which exponential expression is equivalent to $\sqrt[7]{b}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $b^{7}$ $\newline$ (B) $b^{\frac{1}{7}}$ $\newline$ (C) $\frac{1}{b^{7}}$ $\newline$ (D) $\frac{1}{b^{\frac{1}{7}}}$

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

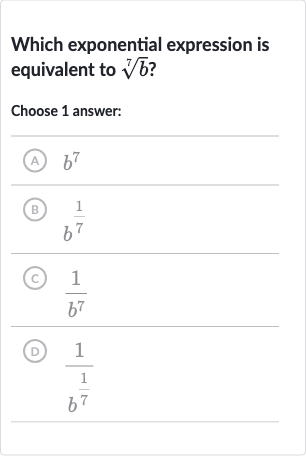
Q. Which exponential expression is equivalent to

\sqrt[7]{b}

?

\newline

Choose

1

answer:

\newline

(A)

b^{7}

\newline

(B)

b^{\frac{1}{7}}

\newline

(C)

\frac{1}{b^{7}}

\newline

(D)

\frac{1}{b^{\frac{1}{7}}}

Understand $7$ th Root of $b$ : Understand the meaning of the $7$ th root of $b$ . The $7$ th root of $b$ is the number that, when raised to the power of $7$ , gives $b$ . This can be written as an exponent by raising $b$ to the power of $\frac{1}{7}$ .
Match with Given Options: Match the $7$ th root of $b$ with the given options. $\newline$ (A) $b^{7}$ means $b$ raised to the power of $7$ , which is not the $7$ th root of $b$ . $\newline$ (B) $b^{\left(\frac{1}{7}\right)}$ means $b$ raised to the power of $\frac{1}{7}$ , which is the $7$ th root of $b$ . $\newline$ (C) $b$ $2$ means the reciprocal of $b$ raised to the power of $7$ , which is not the $7$ th root of $b$ . $\newline$ (D) $b$ $7$ means the reciprocal of $b$ raised to the power of $\frac{1}{7}$ , which is not the $7$ th root of $b$ .
Choose Correct Answer: Choose the correct answer. $\newline$ The correct exponential expression that is equivalent to the $7$ th root of $b$ is $b$ raised to the power of $\frac{1}{7}$ . $\newline$ So, the correct answer is (B) $b^{\left(\frac{1}{7}\right)}$ .

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 3 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 3 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 2 months ago

Question

\newline

32^{(-1/5)}

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 2 months ago