Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which exponential expression is equivalent to
root(5)(c) ?
Choose 1 answer:
(A)
c^(5)
(B)
(1)/(c^(5))
(c)
(1)/(c^((1)/(5)))
(D)
(1)/(c^(5))

Which exponential expression is equivalent to $\sqrt[5]{c}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $c^{5}$ $\newline$ (B) $\frac{1}{c^{5}}$ $\newline$ (C) $\frac{1}{c^{\frac{1}{5}}}$ $\newline$ (D) $\frac{1}{c^{5}}$

View step-by-step help

View step-by-step help

Identify equivalent linear expressions

Full solution

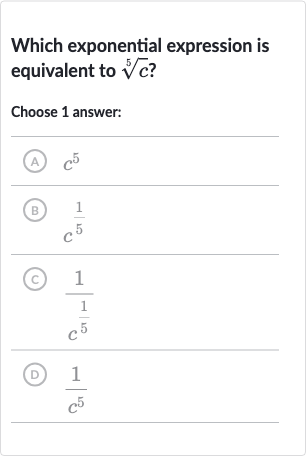
Q. Which exponential expression is equivalent to

\sqrt[5]{c}

?

\newline

Choose

1

answer:

\newline

(A)

c^{5}

\newline

(B)

\frac{1}{c^{5}}

\newline

(C)

\frac{1}{c^{\frac{1}{5}}}

\newline

(D)

\frac{1}{c^{5}}

Understand the meaning: Understand the meaning of the $5$ th root of $c$ . The $5$ th root of $c$ is the number that, when raised to the power of $5$ , gives $c$ . This can be written as $c^{(1/5)}$ .
Match with choices: Match the $5^{\text{th}}$ root of $c$ with the given choices. $\newline$ (A) $c^{5}$ is $c$ raised to the power of $5$ , not the $5^{\text{th}}$ root of $c$ . $\newline$ (B) $\frac{1}{c^{5}}$ is the reciprocal of $c$ raised to the power of $5$ , not the $5^{\text{th}}$ root of $c$ . $\newline$ (C) $c$ $2$ is the reciprocal of the $5^{\text{th}}$ root of $c$ , which is the correct expression for the $5^{\text{th}}$ root of $c$ . $\newline$ (D) $\frac{1}{c^{5}}$ is repeated from choice (B) and is incorrect for the same reason.

More problems from Identify equivalent linear expressions

Question

Evaluate the expression for

j = 7

\newline

2j =

Posted 3 months ago

Question

Evaluate the expression for

y = 4

z = 5

\newline

yz =

Posted 2 months ago

Question

Evaluate the expression for

t = 0

\newline

|-4 - t| =

Posted 3 months ago

Question

8

pictures. Belle drew

p

fewer pictures than Dale. Choose the expression that shows how many pictures Belle drew.

\newline

\newline

8

\newline

p - 8

\newline

8 + p

\newline

8 - p

Posted 3 months ago

Question

Write an expression for the sequence of operations described below. subtract

5

6

w

to the result Do not simplify any part of the expression. ______

Posted 3 months ago

Question

Write an expression for the operation described below.

\newline

4

a

\newline

Posted 3 months ago

Question

12

cookies. Alice baked

n

fewer cookies than John.

\newline

Choose the expression that shows how many cookies Alice baked.

\newline

\newline

12

\newline

n - 12

\newline

12 + n

\newline

12 - n

Posted 4 months ago

Question

15

books. Lucas read

b

fewer books than Emma. Choose the expression that shows how many books Lucas read.

\newline

\newline

15

\newline

b - 15

\newline

15 + b

\newline

15 - b

Posted 4 months ago

Question

10

miles. Sarah ran

m

fewer miles than Max. Choose the expression that shows how many miles Sarah ran.

\newline

\newline

(A)10

\newline

(B)m - 10

\newline

(C)10 + m

\newline

(D)10 - m

Posted 4 months ago

Question

20

poems. Fiona wrote

p

fewer poems than Carlos. Choose the expression that shows how many poems Fiona wrote.

\newline

\newline

20

\newline

p - 20

\newline

20 + p

\newline

20 - p

Posted 4 months ago