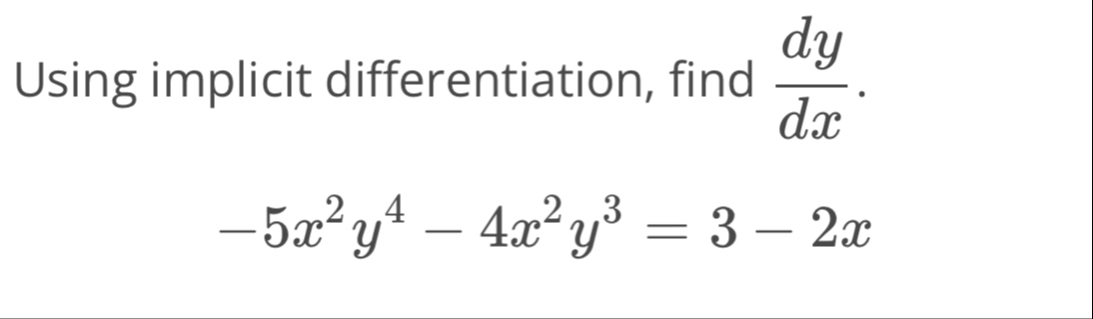Using implicit differentiation, find $\frac{d y}{d x}$ . $\newline$ $-5 x^{2} y^{4}-4 x^{2} y^{3}=3-2 x$

View step-by-step help

Home

Math Problems

Algebra 2

Simplify expressions using trigonometric identities

Full solution

Q. Using implicit differentiation, find

\frac{d y}{d x}

\newline

-5 x^{2} y^{4}-4 x^{2} y^{3}=3-2 x

Differentiate Equation: Differentiate both sides of the equation with respect to $x$ , remembering to use the product rule for terms involving both $x$ and $y$ , and the chain rule for terms involving $y$ since $y$ is a function of $x$ .
Left Side Derivative: Differentiate the left side of the equation. The derivative of $-5x^2y^4$ with respect to $x$ is $-10xy^4 - 20x^2y^3\frac{dy}{dx}$ using the product rule. The derivative of $-4x^2y^3$ with respect to $x$ is $-8xy^3 - 12x^2y^2\frac{dy}{dx}$ using the product rule.
Right Side Derivative: Differentiate the right side of the equation. The derivative of $3$ with respect to $x$ is $0$ , and the derivative of $-2x$ with respect to $x$ is $-2$ .
Write Differentiated Equation: Write down the differentiated equation from Steps $2$ and $3$ : $-10x y^4 - 20x^2 y^3 \frac{dy}{dx} - 8x y^3 - 12x^2 y^2 \frac{dy}{dx} = -2$ .
Collect Terms: Collect all terms involving $\frac{dy}{dx}$ on one side and move all other terms to the opposite side. This gives us $-20x^2y^3\frac{dy}{dx} - 12x^2y^2\frac{dy}{dx} = -2 + 10xy^4 + 8xy^3$ .
Factor Out $(\frac{dy}{dx}):</b> Factor out \$(\frac{dy}{dx})$ from the left side of the equation to get $(\frac{dy}{dx})(-20x^2y^3 - 12x^2y^2) = -2 + 10xy^4 + 8xy^3$ .
Solve for $(\frac{dy}{dx}):</b> Solve for \$(\frac{dy}{dx})$ by dividing both sides of the equation by $(-20x^2y^3 - 12x^2y^2)$ . This gives us $(\frac{dy}{dx}) = \frac{-2 + 10xy^4 + 8xy^3}{-20x^2y^3 - 12x^2y^2}$ .
Simplify $(\frac{dy}{dx}):</b> Simplify the expression for \$(\frac{dy}{dx})$ if possible. In this case, we can factor out an $x$ from the numerator and an $x^2y^2$ from the denominator to get $(\frac{dy}{dx}) = \frac{-2/x + 10y^4 + 8y^3}{-20xy^3 - 12y^2}$ .

Using implicit differentiation, find dydx \frac{d y}{d x} dxdy​.\newline−5x2y4−4x2y3=3−2x -5 x^{2} y^{4}-4 x^{2} y^{3}=3-2 x −5x2y4−4x2y3=3−2x

Using implicit differentiation, find $\frac{d y}{d x}$ . $\newline$ $-5 x^{2} y^{4}-4 x^{2} y^{3}=3-2 x$