Resources

Testimonials

Plans

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

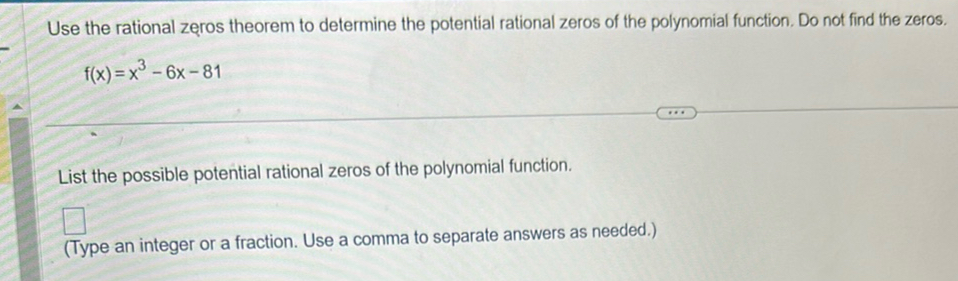
$Use the rational zeros theorem to determine the potential rational zeros of the polynomial function. Do not find the zeros. f(x)=x^(3)-6x-81 List the possible potential rational zeros of the polynomial function. ◻ (Type an integer or a fraction. Use a comma to separate answers as needed.)$

Use the rational zeros theorem to determine the potential rational zeros of the polynomial function. Do not find the zeros. $\newline$ $f(x)=x^{3}-6 x-81$ $\newline$ List the possible potential rational zeros of the polynomial function. $\newline$ $\square$ (Type an integer or a fraction. Use a comma to separate answers as needed.)

View step-by-step help

Home

Math Problems

Algebra 2

Conjugate root theorems

Full solution

Q. Use the rational zeros theorem to determine the potential rational zeros of the polynomial function. Do not find the zeros.

\newline

f(x)=x^{3}-6 x-81

\newline

List the possible potential rational zeros of the polynomial function.

\newline

\square

(Type an integer or a fraction. Use a comma to separate answers as needed.)

Rational Zeros Theorem: The Rational Zeros Theorem states that if a polynomial has integer coefficients, then every rational zero, $\frac{p}{q}$ (in lowest terms), has $p$ as a factor of the constant term and $q$ as a factor of the leading coefficient. $\newline$ For the polynomial $f(x) = x^3 - 6x^2 - 81$ , the constant term is $-81$ and the leading coefficient is $1$ .
Constant Term Factors: List all the factors of the constant term, $-81$ . The factors of $-81$ are $\pm1$ , $\pm3$ , $\pm9$ , $\pm27$ , and $\pm81$ .
Leading Coefficient Factors: List all the factors of the leading coefficient, $1$ . The factors of $1$ are $\pm1$ .
Potential Rational Zeros Calculation: According to the Rational Zeros Theorem, the potential rational zeros are the factors of the constant term divided by the factors of the leading coefficient. Since the leading coefficient is $1$ , the potential rational zeros are simply the factors of the constant term.
Combine Factors for Zeros: Combine the factors of the constant term to list the potential rational zeros. The potential rational zeros are $\pm 1$ , $\pm 3$ , $\pm 9$ , $\pm 27$ , and $\pm 81$ .