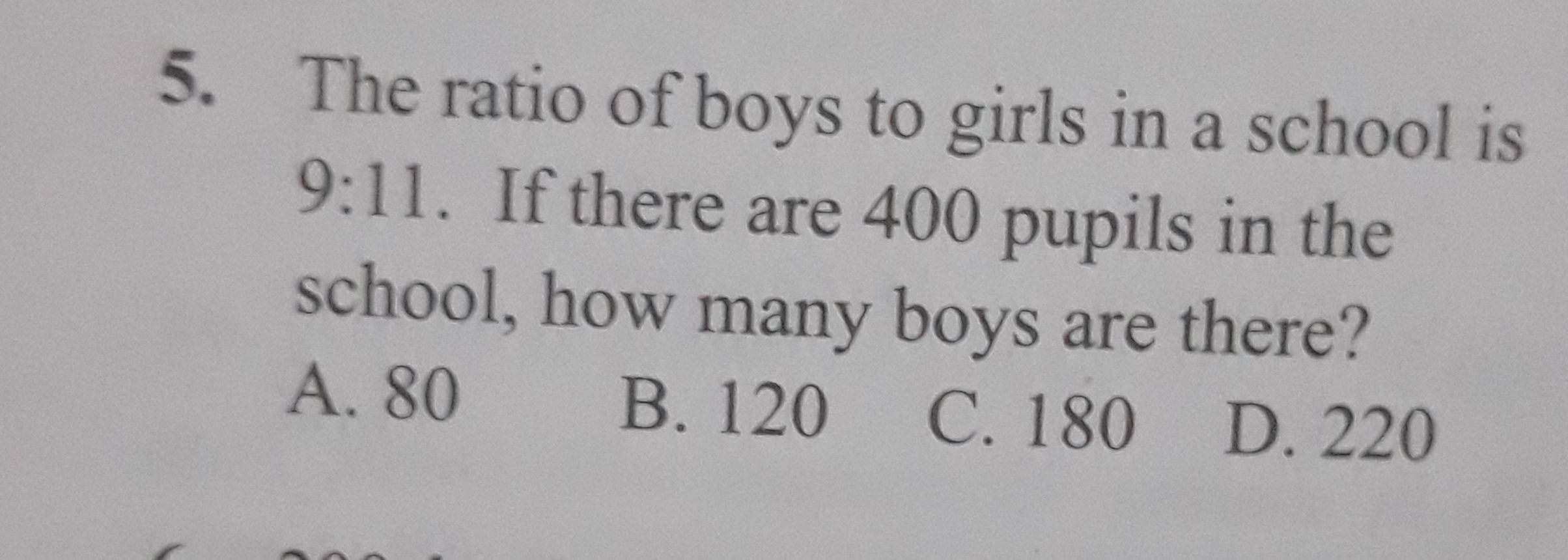Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The ratio of boys to girls in a school is
9:11. If there are 400 pupils in the school, how many boys are there?
A. 80
B. 120
C. 180
D. 220

The ratio of boys to girls in a school is $9: 11$ . If there are $400$ pupils in the school, how many boys are there? $\newline$ A. $80$ $\newline$ B. $120$ $\newline$ C. $180$ $\newline$ D. $220$

View step-by-step help

View step-by-step help

Exponential growth and decay: word problems

Full solution

Q. The ratio of boys to girls in a school is

9: 11

. If there are

400

pupils in the school, how many boys are there?

\newline

A.

80

\newline

B.

120

\newline

C.

180

\newline

D.

220

Denote Boys and Girls: Let's denote the number of boys as $B$ and the number of girls as $G$ . According to the problem, the ratio of boys to girls is $9:11$ , which can be written as $\frac{B}{G} = \frac{9}{11}$ .
Ratio and Total Number: We also know that the total number of pupils is the sum of the number of boys and girls, which is $B + G = 400$ .
Express in Terms of Ratio: To find the number of boys, we need to express both $B$ and $G$ in terms of the ratio $9:11$ . Let's introduce a variable $k$ such that $B = 9k$ and $G = 11k$ . This maintains the ratio of boys to girls.
Substitute in Equation: Now we can substitute $B$ and $G$ in the total number of pupils equation: $9k + 11k = 400$ .
Combine Like Terms: Combining like terms, we get $20k = 400$ .
Find Value of k: To find the value of k, we divide both sides of the equation by $20$ : $k = \frac{400}{20}$ .
Calculate k Value: Calculating the value of $k$ , we get $k = 20$ .
Find Number of Boys: Now that we have the value of $k$ , we can find the number of boys by substituting $k$ back into $B = 9k$ : $B = 9 \times 20$ .
Calculate Boys: Calculating the number of boys, we get $B = 180$ .

More problems from Exponential growth and decay: word problems

Question

Solve. Write your answer as an integer or a fraction in simplest form.

\newline

5^x=1

\newline

x=

Posted 3 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

Posted 3 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

\newline

f(1) =

Posted 2 months ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = 9^x

\newline

x =

Posted 3 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 1 month ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 3 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 2 months ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 3 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6^x

\newline

f(x) = 6x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 3 months ago