AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
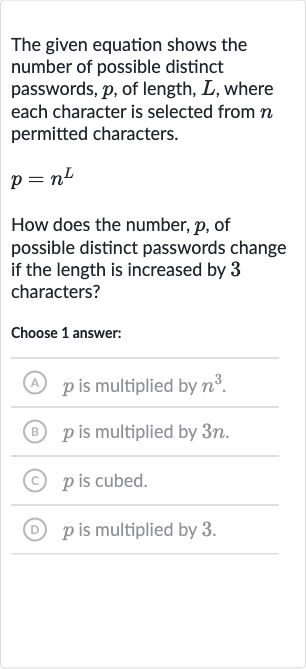
The given equation shows the number of possible distinct passwords, , of length, , where each character is selected from permitted characters.How does the number, , of possible distinct passwords change if the length is increased by characters?Choose answer:(A) is multiplied by .(B) is multiplied by .(C) is cubed.(D) is multiplied by .
Full solution
Q. The given equation shows the number of possible distinct passwords, , of length, , where each character is selected from permitted characters.How does the number, , of possible distinct passwords change if the length is increased by characters?Choose answer:(A) is multiplied by .(B) is multiplied by .(C) is cubed.(D) is multiplied by .
- Original Formula Explanation: The original formula for the number of possible distinct passwords is . We need to determine the new number of passwords when the length is increased by .
- New Length Denotation: Let's denote the new length as . The new number of possible passwords will be .
- Substitution of New Length: Substitute into the formula: .
- Rewriting Using Exponents: Using the properties of exponents, we can rewrite as .
- Substitution of Original Number: Since is the original number of passwords , we can substitute back into the equation: .
- Final Conclusion: This shows that the new number of passwords is the original number of passwords multiplied by . Therefore, the correct answer is (A) is multiplied by .
More problems from Find a value using two-variable equations: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
