Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The derivative of the function
f is defined by
f^(')(x)=x^(2)+5cos(3x). Find the
x values, if any, in the interval
-2 < x < 2.5 where the function
f has a relative maximum. You may use a calculator and round all values to 3 decimal places.
Answer:
x=

The derivative of the function $f$ is defined by $f^{\prime}(x)=x^{2}+5 \cos (3 x)$ . Find the $x$ values, if any, in the interval $-2<x<2.5$ where the function $f$ has a relative maximum. You may use a calculator and round all values to $3$ decimal places. $\newline$ Answer: $x=$

View step-by-step help

View step-by-step help

Find derivatives using logarithmic differentiation

Full solution

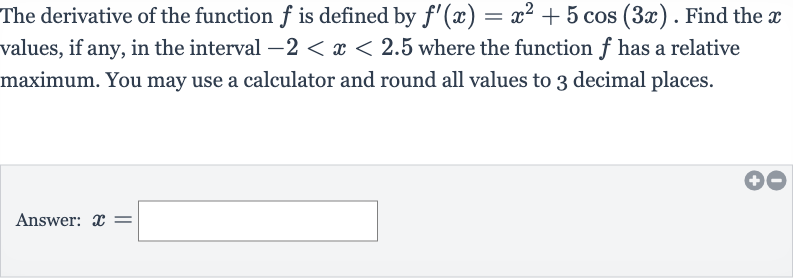
Q. The derivative of the function

f

is defined by

f^{\prime}(x)=x^{2}+5 \cos (3 x)

. Find the

x

values, if any, in the interval

-2<x<2.5

where the function

f

has a relative maximum. You may use a calculator and round all values to

3

decimal places.

\newline

Answer:

x=

Find Critical Points: To find the relative maximum of the function $f$ , we need to find the critical points of $f^{\prime}(x)$ in the given interval. Critical points occur where the derivative is zero or undefined.
Set Derivative Equal: First, we set the derivative equal to zero to find potential critical points: $f'(x) = x^{2} + 5\cos(3x) = 0$
Solve for $x$ : We solve for $x$ using a calculator, as the equation involves both polynomial and trigonometric terms: $\newline$ $x^{2} + 5\cos(3x) = 0$
Use Calculator: Since the equation is transcendental and cannot be solved algebraically, we use numerical methods or a graphing calculator to find the approximate values of $x$ in the interval $-2 < x < 2.5$ .
Determine Maxima: After using a calculator, we find that the approximate values of $x$ that satisfy the equation are $x \approx -1.439$ , $x \approx 0.960$ , and $x \approx 2.172$ (rounded to three decimal places).
Apply First Derivative Test: Next, we need to determine which of these critical points are relative maxima. To do this, we can use the first derivative test, which involves checking the sign of the derivative before and after each critical point.
Check Sign Change: We plug in values slightly less and slightly more than $x \approx -1.439$ , $x \approx 0.960$ , and $x \approx 2.172$ into the derivative to check the sign change.
Relative Maximums: For $x \approx -1.439$ , we find that the derivative changes from positive to negative, indicating a relative maximum at this point.
Relative Maximums: For $x \approx -1.439$ , we find that the derivative changes from positive to negative, indicating a relative maximum at this point.For $x \approx 0.960$ , we find that the derivative changes from negative to positive, indicating a relative minimum at this point, so we discard it.
Relative Maximums: For $x \approx -1.439$ , we find that the derivative changes from positive to negative, indicating a relative maximum at this point.For $x \approx 0.960$ , we find that the derivative changes from negative to positive, indicating a relative minimum at this point, so we discard it.For $x \approx 2.172$ , we find that the derivative changes from positive to negative, indicating a relative maximum at this point.
Relative Maximums: For $x \approx -1.439$ , we find that the derivative changes from positive to negative, indicating a relative maximum at this point.For $x \approx 0.960$ , we find that the derivative changes from negative to positive, indicating a relative minimum at this point, so we discard it.For $x \approx 2.172$ , we find that the derivative changes from positive to negative, indicating a relative maximum at this point.Therefore, the function $f$ has relative maxima at $x \approx -1.439$ and $x \approx 2.172$ within the interval $-2 < x < 2.5$ .

More problems from Find derivatives using logarithmic differentiation

Question

\newline

\sqrt{\frac{9}{25}}

\newline

Posted 3 months ago

Question

\newline

1,000

\text{ milligrams}

\_\_\_\_

\text{ grams}

Posted 3 months ago

Question

3

-gallon bottle of bleach costs

\$11.52

. What is the price per quart?

\newline

Posted 3 months ago

Question

Maureen can't wait to make chocolate chip zucchini bread with zucchini from her garden. Her recipe calls for

8

ounces of chocolate chips per loaf. If she has enough zucchini to make

4

loaves of zucchini bread, how many pounds of chocolate chips does she need?

\newline

Hint: There are

16

1

\newline

Write your answer as a whole number, decimal, or simplified fraction. Do not round.

\newline

Posted 3 months ago

Question

A whale is swimming due north at a speed of

30

miles per hour. Just

5

miles away, a whale-watching tour boat is traveling south, directly toward the whale, at a speed of

46

miles per hour. How long will it be before they meet? If necessary, round your answer to the nearest minute.

\_\_\_\_

\_\_\_\_

Posted 3 months ago

Question

\newline

500

=

Posted 4 months ago

Question

\newline

2,000

=

Posted 4 months ago

Question

\newline

750

=

Posted 4 months ago

Question

\newline

1,500

=

Posted 4 months ago

Question

\newline

1,500

=

Posted 4 months ago