Suppose that $\sin \alpha=\frac{3}{\sqrt{13}}$ and $0^{\circ}<\alpha<90^{\circ}$ $\newline$ Find the exact values of $\cos \frac{\alpha}{2}$ and $\tan \frac{\alpha}{2}$ . $\newline$ $\cos \frac{\alpha}{2}=$ $\newline$ $\tan \frac{\alpha}{2}=$

View step-by-step help

Home

Math Problems

Algebra 2

Evaluate functions

Full solution

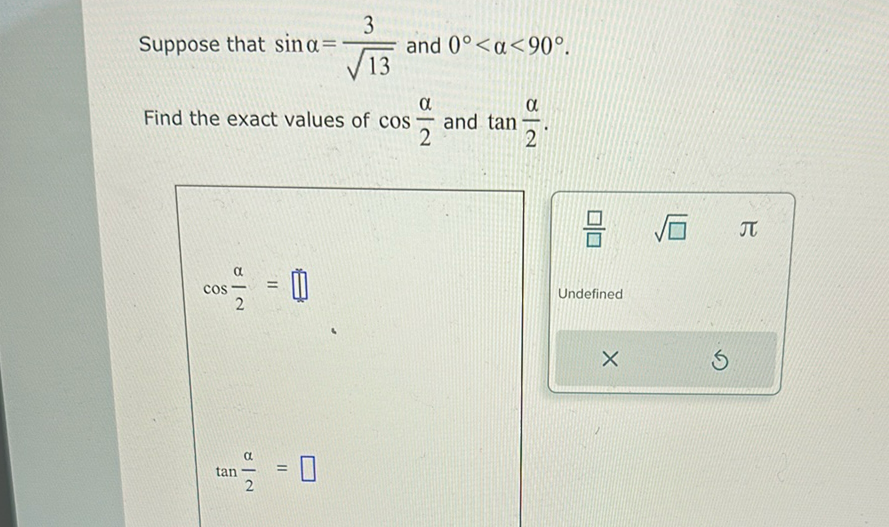
Q. Suppose that

\sin \alpha=\frac{3}{\sqrt{13}}

and

0^{\circ}<\alpha<90^{\circ}

\newline

Find the exact values of

\cos \frac{\alpha}{2}

and

\tan \frac{\alpha}{2}

\newline

\cos \frac{\alpha}{2}=

\newline

\tan \frac{\alpha}{2}=

Given Information: We are given that $\sin(\alpha) = \frac{3}{\sqrt{13}}$ and $\alpha$ is in the first quadrant $(0^\circ < \alpha < 90^\circ)$ . To find $\cos(\alpha/2)$ and $\tan(\alpha/2)$ , we can use the half-angle formulas for sine and cosine. The half-angle formula for cosine is: $\newline$ $\cos(\alpha/2) = \pm\sqrt{\left(\frac{1 + \cos(\alpha)}{2}\right)}$ $\newline$ Since $\alpha$ is in the first quadrant, $\cos(\alpha)$ will be positive, and since we are looking for $\cos(\alpha/2)$ in the first or second quadrant (because $\alpha/2$ will be less than $90^\circ$ ), we will choose the positive square root. $\newline$ First, we need to find $\cos(\alpha)$ using the Pythagorean identity: $\newline$ $\cos^2(\alpha) + \sin^2(\alpha) = 1$ $\newline$ $\cos^2(\alpha) = 1 - \sin^2(\alpha)$ $\newline$ $\cos^2(\alpha) = 1 - \left(\frac{3}{\sqrt{13}}\right)^2$ $\newline$ $\cos^2(\alpha) = 1 - \frac{9}{13}$ $\newline$ $\cos^2(\alpha) = \frac{13}{13} - \frac{9}{13}$ $\newline$ $\cos^2(\alpha) = \frac{4}{13}$ $\newline$ $\alpha$ $1$ $\newline$ $\alpha$ $2$
Find $\cos(\alpha/2)$ : Now we can find $\cos(\alpha/2)$ using the half-angle formula: $\newline$ $\cos(\alpha/2) = \pm\sqrt{(1 + \cos(\alpha))/2}$ $\newline$ $\cos(\alpha/2) = \sqrt{(1 + 2/\sqrt{13})/2}$ $\newline$ $\cos(\alpha/2) = \sqrt{(\sqrt{13}/\sqrt{13} + 2/\sqrt{13})/2}$ $\newline$ $\cos(\alpha/2) = \sqrt{(\sqrt{13} + 2)/2\sqrt{13}}$ $\newline$ $\cos(\alpha/2) = \sqrt{(\sqrt{13} + 2)/(2\sqrt{13})}$ $\newline$ $\cos(\alpha/2) = \sqrt{(\sqrt{13} + 2)\sqrt{13}/(2\sqrt{13}\sqrt{13})}$ $\newline$ $\cos(\alpha/2) = \sqrt{(\sqrt{13} + 2)\sqrt{13}/(26)}$ $\newline$ $\cos(\alpha/2) = \sqrt{(13 + 2\sqrt{13})/26}$ $\newline$ $\cos(\alpha/2) = \sqrt{(13 + 2\sqrt{13})/26}$
Find $\tan(\alpha/2)$ : Next, we will find $\tan(\alpha/2)$ using the half-angle formula for tangent, which is: $\newline$ $\tan(\alpha/2) = \pm\sqrt{(1 - \cos(\alpha))/(1 + \cos(\alpha))}$ $\newline$ Since $\alpha$ is in the first quadrant, $\tan(\alpha)$ will be positive, and we will choose the positive square root for $\tan(\alpha/2)$ . $\newline$ $\tan(\alpha/2) = \sqrt{(1 - \cos(\alpha))/(1 + \cos(\alpha))}$ $\newline$ $\tan(\alpha/2) = \sqrt{(1 - 2/\sqrt{13})/(1 + 2/\sqrt{13})}$ $\newline$ $\tan(\alpha/2) = \sqrt{(\sqrt{13}/\sqrt{13} - 2/\sqrt{13})/(\sqrt{13}/\sqrt{13} + 2/\sqrt{13})}$ $\newline$ $\tan(\alpha/2) = \sqrt{(\sqrt{13} - 2)/(\sqrt{13} + 2)}$ $\newline$ $\tan(\alpha/2)$ $0$ $\newline$ $\tan(\alpha/2)$ $1$ $\newline$ $\tan(\alpha/2)$ $1$