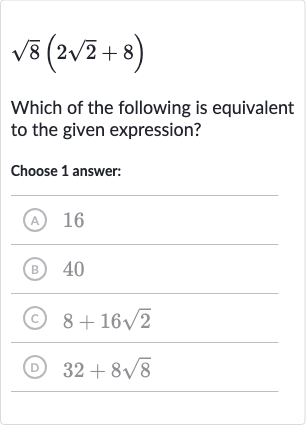
Full solution
Q. Which of the following is equivalent to the given expression?Choose answer:(A) (B) (C) (D)
- Simplify expression inside parentheses: First, we will simplify the expression inside the parentheses by multiplying the square root of with each term inside the parentheses. The expression is .
- Calculate first term: We calculate the first term by multiplying with , which gives us . Since , we can simplify the expression to .
- Simplify first term: We know that . So, the first term becomes , which equals .
- Calculate second term: Now, we calculate the second term by multiplying with . Since we already know that , the second term becomes .
- Multiply second term: Multiplying by gives us . So, the second term is .
- Add the two terms: Adding the two terms together, we get . This is the simplified form of the original expression.
- Compare with answer choices: Comparing the simplified expression with the answer choices, we find that it matches with option (C) .
More problems from Is (x, y) a solution to the system of equations?
QuestionGet tutor help
QuestionGet tutor help