Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve the following equation for
x. Express your answer in the simplest form.

4(-2x-1)=-2(4x+2)

Solve the following equation for $x$ . Express your answer in the simplest form. $\newline$ $4(-2 x-1)=-2(4 x+2)$ $\newline$

View step-by-step help

View step-by-step help

Evaluate expression when two complex numbers are given

Full solution

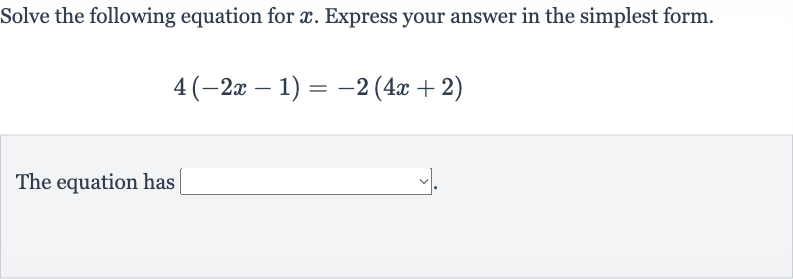
Q. Solve the following equation for

x

. Express your answer in the simplest form.

\newline

4(-2 x-1)=-2(4 x+2)

\newline

Distribute Numbers: We are given the equation: $\newline$ $4(-2x - 1) = -2(4x + 2)$ $\newline$ First, we need to distribute the numbers outside the parentheses to the terms inside.
Left Side Calculation: Distribute $4$ to the terms inside the first set of parentheses: $\newline$ $4 \times -2x = -8x$ $\newline$ $4 \times -1 = -4$ $\newline$ So, the left side of the equation becomes: $\newline$ $-8x - 4$
Right Side Calculation: Distribute $-2$ to the terms inside the second set of parentheses: $\newline$ $-2 \times 4x = -8x$ $\newline$ $-2 \times 2 = -4$ $\newline$ So, the right side of the equation becomes: $\newline$ $-8x - 4$
Equation Comparison: Now, the equation looks like this: $\newline$ $-8x - 4 = -8x - 4$ $\newline$ Next, we can try to isolate $x$ , but we notice that both sides of the equation are identical.
Infinite Solutions: Since both sides of the equation are the same, any value of $x$ will satisfy the equation. This means the equation has infinitely many solutions.

More problems from Evaluate expression when two complex numbers are given

Question

\newline

8i + 6i

\newline

\newline

Write your answer in the form

a + bi

\newline

\underline{\hspace{1cm}}

\newline

Posted 2 months ago

Question

Find the complex conjugate of the given number.

\newline

4 + 10i

\newline

\newline

Write your answer in the form

a + bi

\newline

Posted 2 months ago

Question

\newline

\frac{{-4i}}{{-9i}}

\newline

\newline

Write your answer in the form

a + bi

. Reduce all fractions.

\newline

\_\_\_\_\_

\newline

Posted 2 months ago

Question

Combine the like terms to create an equivalent expression.

\newline

7k-k+19=\boxed{\phantom{0}}

Posted 4 months ago

Question

Apply the distributive property to factor out the greatest common factor.

\newline

9+12 n=

Posted 1 month ago

Question

Solve the equation.

\newline

\begin{aligned} & 12=n-9 \\ n= & \square \end{aligned}

Posted 4 months ago

Question

What is the amplitude of

y=-\sin (8 x-3)+5

\newline

Posted 2 months ago

Question

What is the period of

\newline

y=4 \sin (-2 x+7)-1 \text { ? }

\newline

Give an exact value.

\newline

Posted 2 months ago

Question

3 \cdot(3+20 i)=

\newline

Your answer should be a complex number in the form

a+b i

a

b

are real numbers.

Posted 4 months ago

Question

(35-23 i)+(13+25 i)=

\newline

Express your answer in the form

(a+b i)

Posted 2 months ago