Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve the following equation for
b. Be sure to take into account whether a letter is capitalized or not.

q=h^(2)(b-n)
Answer:
b=

Solve the following equation for $b$ . Be sure to take into account whether a letter is capitalized or not. $\newline$ $q=h^{2}(b-n)$ $\newline$ Answer: $b=$

View step-by-step help

View step-by-step help

Write and solve direct variation equations

Full solution

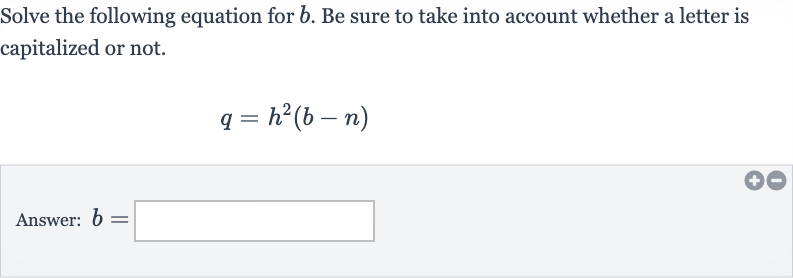
Q. Solve the following equation for

b

. Be sure to take into account whether a letter is capitalized or not.

\newline

q=h^{2}(b-n)

\newline

Answer:

b=

Isolate term with b: Isolate the term containing b. $\newline$ To solve for b, we need to isolate it on one side of the equation. We start by dividing both sides of the equation by $h^2$ to get rid of the $h^2$ term on the right side. $\newline$ $q = h^2(b - n)$ $\newline$ Divide both sides by $h^2$ : $\newline$ $q / h^2 = (h^2(b - n)) / h^2$
Divide and simplify: Simplify the equation. $\newline$ After dividing both sides by $h^2$ , the $h^2$ terms on the right side cancel out, leaving us with: $\newline$ $\frac{q}{h^2} = b - n$
Solve for b: Solve for b. $\newline$ To solve for b, we need to get b by itself. We do this by adding $n$ to both sides of the equation: $\newline$ $\left(\frac{q}{h^2}\right) + n = b - n + n$
Final equation: Simplify the equation further. $\newline$ After adding $n$ to both sides, the $-n$ and $+n$ on the right side cancel each other out, leaving us with the final equation for $b$ : $\newline$ $b = (q / h^2) + n$

More problems from Write and solve direct variation equations

Question

In a direct variation,

y = 6

x = 2

. Write a direct variation equation that shows the relationship between

x

y

\newline

Write your answer as an equation with

y

first, followed by an equals sign.

Posted 3 months ago

Question

y

varies directly with

x

y = 12

x = 6

y

x = 4

\newline

Write and solve a direct variation equation to find the answer.

\newline

y =

Posted 2 months ago

Question

Which equation shows inverse variation?

\newline

\newline

(\frac{x}{36}) = y

\newline

yx = -74

Posted 3 months ago

Question

y

varies inversely with

x

y = 1

x = 4

y

x = 2

\newline

Write and solve an inverse variation equation to find the answer.

\newline

y =

Posted 2 months ago

Question

What is the value of

\frac{x^{2}}{y^{4}}

x=8

y=2

Posted 22 days ago

Question

(x+4)(2 x-a)=0

\newline

In the given equation,

a

is a constant. If the equation has the solutions

x=4

x=-4

, what is the value of

a

Posted 2 months ago

Question

(2 x+5)(-m x+9)=0

\newline

In the given equation,

m

is a constant. If the equation has the solutions

x=-\frac{5}{2}

x=\frac{3}{2}

, what is the value of

m

Posted 2 months ago

Question

(4 x+3)-(5 x-7)=a x+b

\newline

In the given equation,

b

is a constant. What is the value of

b

Posted 2 months ago

Question

y=\frac{29}{8} x-\frac{2}{3}

\newline

The given equation is graphed in the

x y

-plane. What is the slope of the line?

Posted 2 months ago

Question

a t^{2}+\frac{7}{2} t-4=0

\newline

The given equation has solutions at

t=-8

t=1

. What is the value of the constant

a

Posted 1 month ago