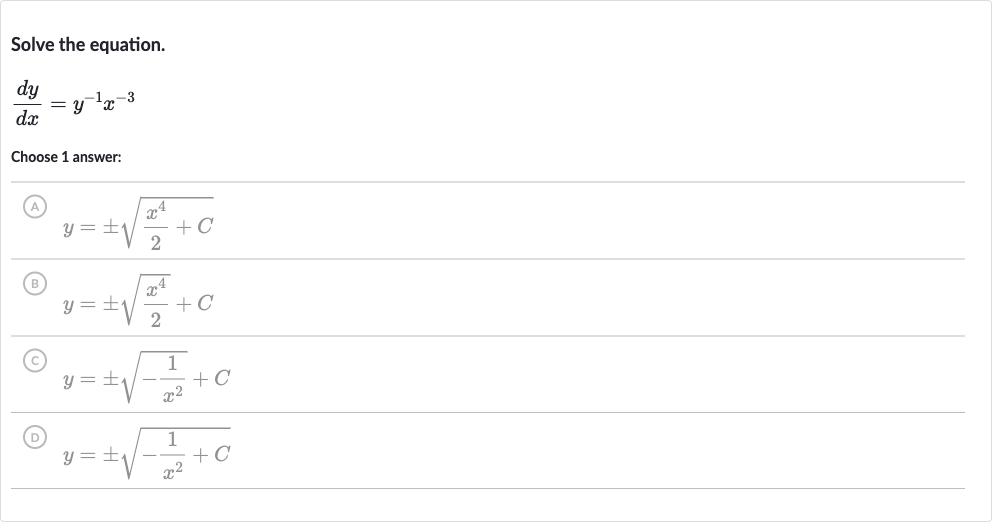
Solve the equation. (dy)/(dx)=y^(-1)x^(-3) Choose 1 answer: (A) y=+-sqrt((x^(4))/(2)+C) (B) y=+-sqrt((x^(4))/(2))+C (C) y=+-sqrt(-(1)/(x^(2)))+C (D) y=+-sqrt(-(1)/(x^(2))+C)

Question

Solve the equation.  (dy)/(dx)=y^(-1)x^(-3) Choose 1 answer: (A)  y=+-sqrt((x^(4))/(2)+C) (B)  y=+-sqrt((x^(4))/(2))+C (C)  y=+-sqrt(-(1)/(x^(2)))+C (D)  y=+-sqrt(-(1)/(x^(2))+C)

Bytelearn · Accepted Answer

Separate Variables: We are given the differential equation (dy)/(dx) = y^(-1)x^(-3). To solve this, we will separate the variables y and x to integrate them separately. Rearrange the equation to separate variables: y * (dy)/(dx) = x^(-3)Integrate Separately: Now integrate both sides with respect to their respective variables: ∫ y dy = ∫ x^(-3) dxPerform Integration: Perform the integration on both sides: (1/2)y^2 = -(1/2)x^(-2) + C where C is the constant of integration.Solve for y: Now we solve for y by taking the square root of both sides: y = ±sqrt(-(1)/(x^2) + C)Check Answer Choices: We check the answer choices to see which one matches our solution: (A) y = ±sqrt((x^(4))/(2) + C) - Incorrect, does not match our solution. (B) y = ±sqrt((x^(4))/(2)) + C - Incorrect, does not match our solution. (C) y = ±sqrt(-(1)/(x^(2))) + C - Incorrect, the constant C should be inside the square root. (D) y = ±sqrt(-(1)/(x^(2)) + C) - Correct, matches our solution.

Solve the equation. $\newline$ $\frac{d y}{d x}=y^{-1} x^{-3}$ $\newline$ Choose $1$ answer: $\newline$ (A) $y= \pm \sqrt{\frac{x^{4}}{2}+C}$ $\newline$ (B) $y= \pm \sqrt{\frac{x^{4}}{2}}+C$ $\newline$ (C) $y= \pm \sqrt{-\frac{1}{x^{2}}}+C$ $\newline$ (D) $y= \pm \sqrt{-\frac{1}{x^{2}}+C}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics