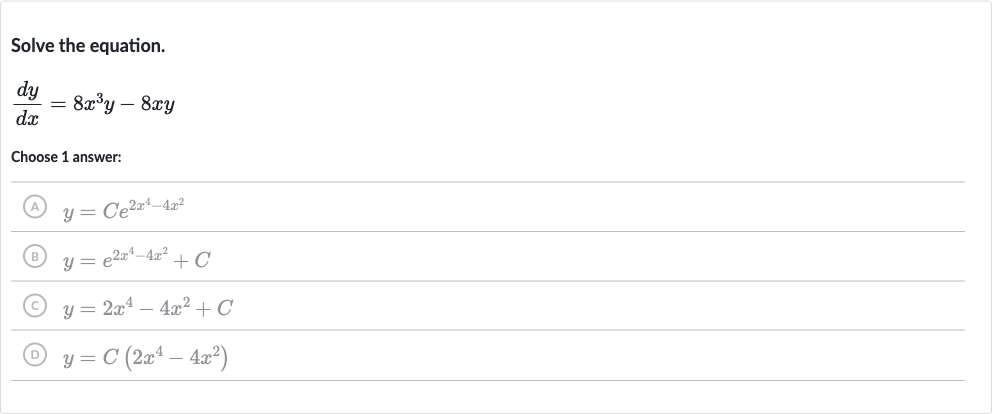
Solve the equation. (dy)/(dx)=8x^(3)y-8xy Choose 1 answer: (A) y=Ce^(2x^(4)-4x^(2)) (B) y=e^(2x^(4)-4x^(2))+C (C) y=2x^(4)-4x^(2)+C (D) y=C(2x^(4)-4x^(2))

Question

Solve the equation.  (dy)/(dx)=8x^(3)y-8xy Choose 1 answer: (A)  y=Ce^(2x^(4)-4x^(2)) (B)  y=e^(2x^(4)-4x^(2))+C (C)  y=2x^(4)-4x^(2)+C (D)  y=C(2x^(4)-4x^(2))

Bytelearn · Accepted Answer

Recognize type of differential equation: Recognize the type of differential equation. The given differential equation is of the form (dy)/(dx) = f(x)y, which suggests it is a first-order linear homogeneous differential equation and can be solved using separation of variables or by recognizing it as a separable differential equation.Separate variables: Separate variables. To solve the equation, we need to separate the variables y and x. We can do this by dividing both sides by y and then dividing by 8x^3 - 8x to get the y terms on one side and the x terms on the other side. (dy)/(y) = (8x^3 - 8x)(dx)Simplify the equation: Simplify the equation. We can factor out 8x from the right side to simplify the equation. (dy)/(y) = 8x(x^2 - 1)(dx)Integrate both sides: Integrate both sides. Now we integrate both sides of the equation to find the solution. ∫(1/y)(dy) = ∫8x(x^2 - 1)(dx) The left side integrates to ln|y|, and the right side requires integration by parts or recognizing it as a standard polynomial integral. ln|y| = ∫8x^3(dx) - ∫8x(dx) ln|y| = 2x^4 - 4x^2 + CSolve for y: Solve for y. To solve for y, we exponentiate both sides of the equation. e^(ln|y|) = e^(2x^4 - 4x^2 + C) y = e^(2x^4 - 4x^2) * e^C Since e^C is just a constant, we can denote it as C'. y = C'e^(2x^4 - 4x^2)Determine correct answer: Determine the correct answer from the given options. Comparing our solution to the answer choices, we see that our solution matches with option (A) if we consider C' as Ce^(2x^4 - 4x^2).

Solve the equation. $\newline$ $\frac{d y}{d x}=8 x^{3} y-8 x y$ $\newline$ Choose $1$ answer: $\newline$ (A) $y=C e^{2 x^{4}-4 x^{2}}$ $\newline$ (B) $y=e^{2 x^{4}-4 x^{2}}+C$ $\newline$ (C) $y=2 x^{4}-4 x^{2}+C$ $\newline$ (D) $y=C\left(2 x^{4}-4 x^{2}\right)$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics