AI tutor
Full solution
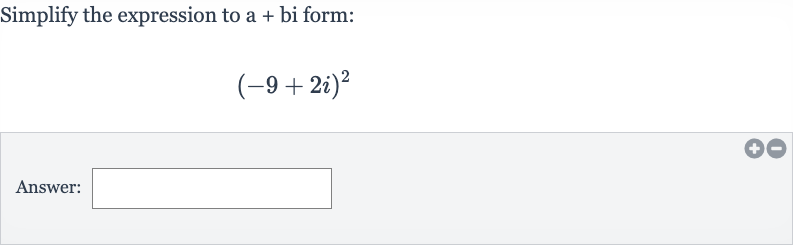
Q. Simplify the expression to a + bi form:Answer:
- Square Real Part: To simplify the expression , we need to square the complex number . This involves using the formula , where and .
- Multiply Real and Imaginary: First, we square the real part , which is . So, .
- Square Imaginary Part: Next, we multiply the real part by the imaginary part by . So, .
- Combine All Parts: Then, we square the imaginary part , which is . So, . Since , this simplifies to .
- Simplify Expression: Now, we combine all the parts together: (from the real part squared) + (from the double product of and ) - (from the imaginary part squared).
- Simplify Expression: Now, we combine all the parts together: (from the real part squared) + (from the double product of and ) - (from the imaginary part squared).Simplifying the expression, we get , which is .
More problems from Simplify variable expressions using properties
QuestionGet tutor help