AI tutor
Full solution
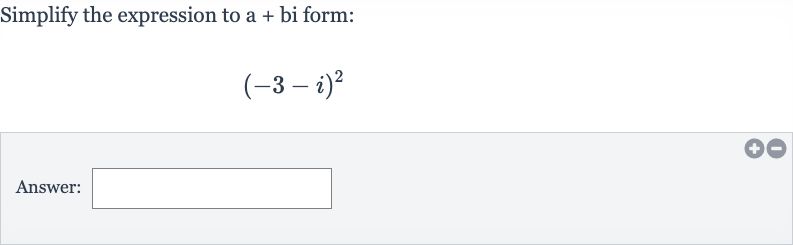
Q. Simplify the expression to a + bi form:Answer:
- Write Expression: Write down the expression to be simplified.We need to square the complex number .
- Apply Formula: Apply the formula to the complex number, where and .
- Calculate Terms: Calculate each term separately. (since )
- Substitute Values: Substitute the calculated values back into the expression.
- Simplify Expression: Simplify the expression by combining like terms.
- Combine Real and Imaginary Parts: Combine the real parts and the imaginary parts.
More problems from Simplify variable expressions using properties
QuestionGet tutor help