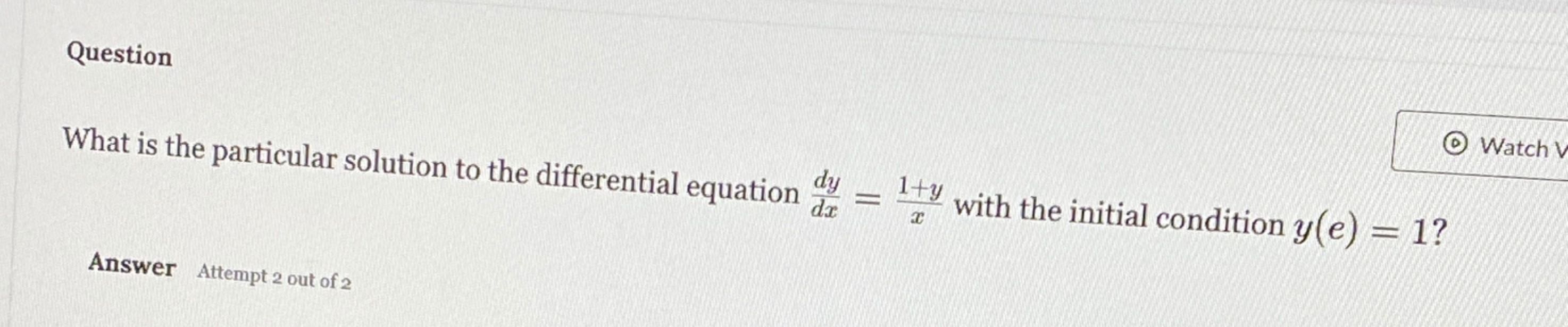Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Question
What is the particular solution to the differential equation
(dy)/(dx)=(1+y)/(x) with the initial condition
y(e)=1 ?

$\newline$ What is the particular solution to the differential equation $\frac{d y}{d x}=\frac{1+y}{x}$ with the initial condition $y(e)=1$ ?

View step-by-step help

View step-by-step help

Simplify expressions using trigonometric identities

Full solution

Q.

\newline

What is the particular solution to the differential equation

\frac{d y}{d x}=\frac{1+y}{x}

with the initial condition

y(e)=1

?

Recognize separable form: Step $1$ : Recognize the differential equation as a separable form. We can write it as $\frac{dy}{1+y} = \frac{dx}{x}$ .
Integrate both sides: Step $2$ : Integrate both sides. The left side becomes $\int \frac{dy}{1+y}$ and the right side becomes $\int \frac{dx}{x}$ .
Perform integration: Step $3$ : Perform the integration. The integral of $\frac{1}{1+y} \, dy$ is $\ln|1+y|$ and the integral of $\frac{1}{x} \, dx$ is $\ln|x|$ . So, $\ln|1+y| = \ln|x| + C$ , where $C$ is the integration constant.
Solve for y: Step $4$ : Solve for y. Exponentiate both sides to remove the logarithm, getting $|1+y| = e^{\ln|x| + C} = |x|e^C$ .
Apply initial condition: Step $5$ : Apply the initial condition $y(e) = 1$ . Substituting $x = e$ and $y = 1$ into $|1+y| = |x|e^C$ gives $|1+1| = |e|e^C$ , so $2 = e^C$ .
Solve for C: Step $6$ : Solve for C. Taking the natural logarithm of both sides, $\ln(2) = C$ .
Substitute back into equation: Step $7$ : Substitute $C$ back into the equation for $y$ . We have $|1+y| = |x|e^{\ln(2)}$ , or $|1+y| = 2|x|$ .
Final solution: Step $8$ : Solve for $y$ . We get $1+y = 2x$ or $y = 2x - 1$ .

More problems from Simplify expressions using trigonometric identities

Question

\cos(\theta)=\frac{8}{17}

0^\circ<\theta<90^\circ

\sec(\theta)

? Write your answer in simplified, rationalized form.

\sec(\theta)=

Posted 3 months ago

Question

\cos(x) = -0.3

\sin(90^\circ - x)

Posted 3 months ago

Question

\csc(\theta) = \frac{17}{8}

0^\circ < \theta < 90^\circ

\tan(\theta)

\newline

Write your answer in simplified, rationalized form.

\newline

\tan(\theta) =

\newline

Posted 3 months ago

Question

Is the sine function even or odd?

\newline

\newline

\text{[A]even}

\newline

\text{[B]odd}

Posted 3 months ago

Question

Write the sentence as an equation.

\newline

89

is equal to the quotient of

y

17

\newline

/

) if you want to use a division sign.

\newline

Posted 2 months ago

Question

Write the sentence as an equation.

\newline

45

is equal to the quotient of

z

5

\newline

/

) if you want to use a division sign.

\newline

Posted 4 months ago

Question

h

\newline

h^2 + 24h = 0

\newline

Write each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.

\newline

h =

Posted 4 months ago

Question

h^2 - 4h = 0

Posted 2 months ago

Question

Combine the like terms to create an equivalent expression:

\newline

-k-(-8k)=\square

Posted 4 months ago

Question

Which of the following degree measures is equal to

5 \pi

\newline

(The number of degrees of arc in a circle is

360

. The number of radians of arc in a circle is

2 \pi

\newline

1

\newline

144^{\circ}

\newline

900^{\circ}

\newline

1,080^{\circ}

\newline

1,800^{\circ}

Posted 2 months ago