Full solution
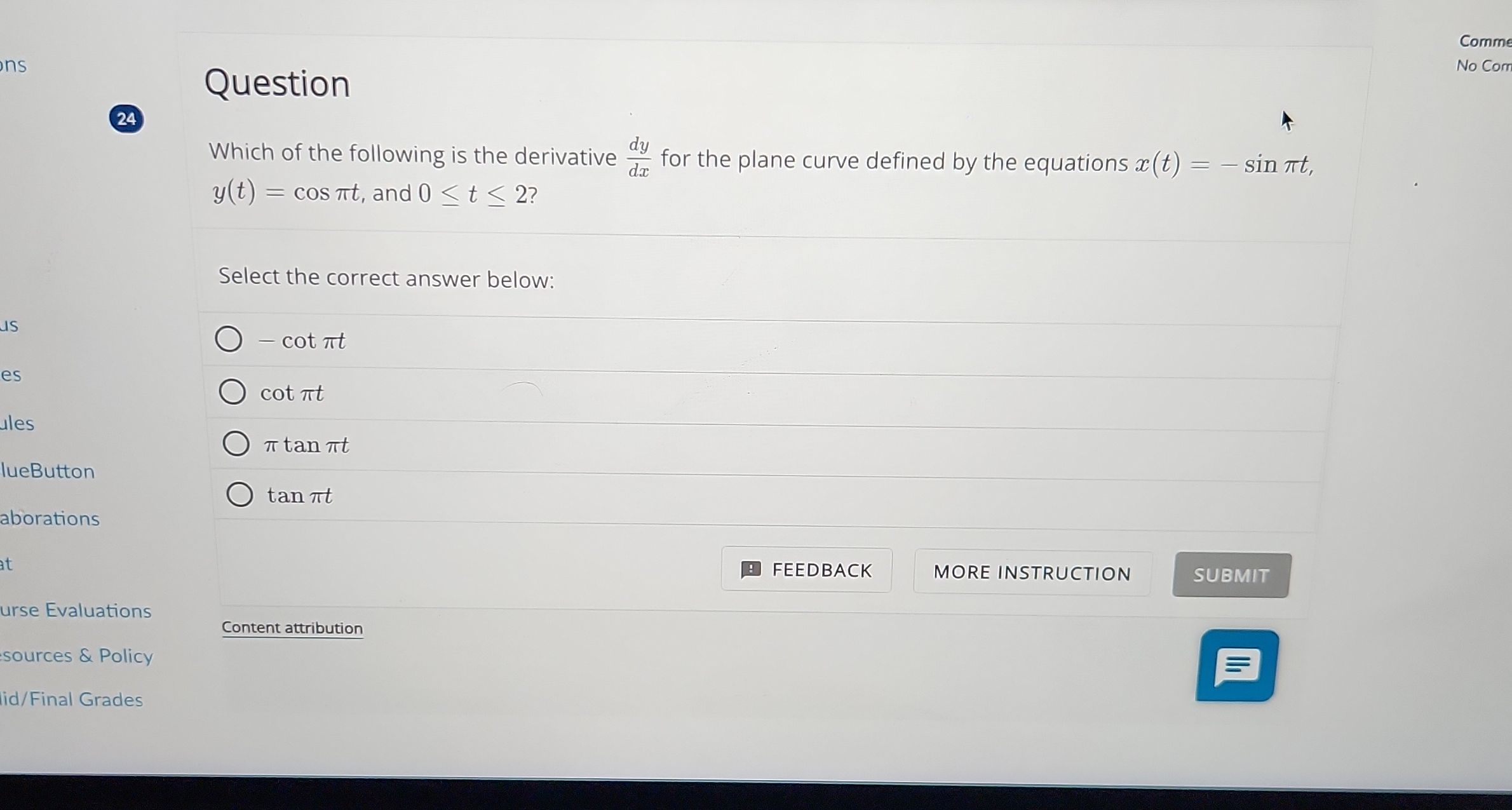
Q. Which of the following is the derivative for the plane curve defined by the equations , , and ?Select the correct answer below:(A) (B) (C) (D)
- Find : To find the derivative , we need to find and first and then divide by .
- Find : Let's find . Given , we differentiate with respect to to get .
- Calculate . Given , we differentiate with respect to to get .
- Simplify the expression: Now we have and . To find , we divide by .
- Final Result: We can simplify the expression by canceling out the terms in the numerator and the denominator.
- Final Result: We can simplify the expression by canceling out the terms in the numerator and the denominator. The expression is the definition of .
More problems from Inverses of sin, cos, and tan: degrees
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help