AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
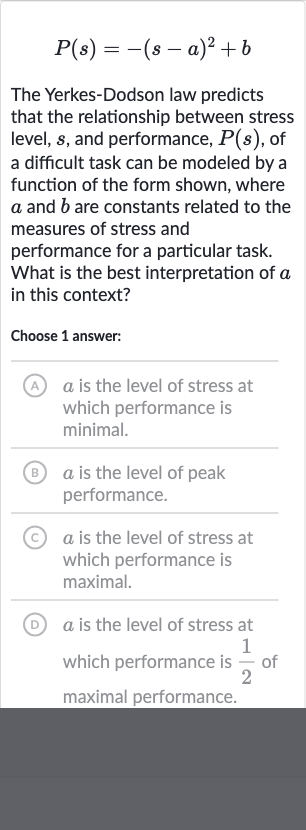
The Yerkes-Dodson law predicts that the relationship between stress level, , and performance, , of a difficult task can be modeled by a function of the form shown, where and are constants related to the measures of stress and performance for a particular task. What is the best interpretation of in this context?Choose answer:(A) is the level of stress at which performance is minimal.(B) is the level of peak performance.(C) is the level of stress at which performance is maximal.(D) is the level of stress at which performance is of maximal performance.
Full solution
Q. The Yerkes-Dodson law predicts that the relationship between stress level, , and performance, , of a difficult task can be modeled by a function of the form shown, where and are constants related to the measures of stress and performance for a particular task. What is the best interpretation of in this context?Choose answer:(A) is the level of stress at which performance is minimal.(B) is the level of peak performance.(C) is the level of stress at which performance is maximal.(D) is the level of stress at which performance is of maximal performance.
- Understand Vertex Form: The Yerkes-Dodson law is represented by the function . To understand the role of the constant in this function, we need to analyze the structure of the equation. This is a quadratic equation in vertex form, where the vertex of the parabola is given by the point . In the context of the Yerkes-Dodson law, the vertex represents the optimal point of performance.
- Interpret Negative Sign: Since the quadratic equation is in the form , the negative sign in front of the squared term indicates that the parabola opens downwards. This means that the vertex is the highest point on the graph. Therefore, at , the performance is at its maximum value, which is .
- Identify Optimal Stress Level: Given that the vertex represents the highest point on the graph and corresponds to the maximum performance level, we can interpret the constant as the level of stress at which performance is maximal. This is because at , the function reaches its maximum value.
