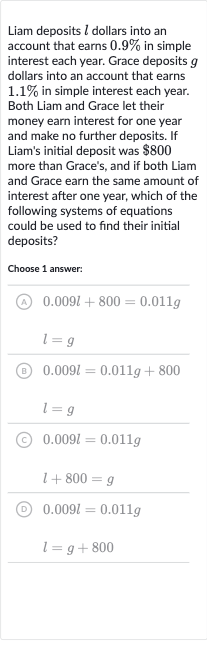
Liam deposits $l$ dollars into an account that earns $0.9 \%$ in simple interest each year. Grace deposits $g$ dollars into an account that earns $1.1 \%$ in simple interest each year. Both Liam and Grace let their money earn interest for one year and make no further deposits. If Liam's initial deposit was $\$ 800$ more than Grace's, and if both Liam and Grace earn the same amount of interest after one year, which of the following systems of equations could be used to find their initial deposits? $\newline$ Choose $1$ answer: $\newline$ (A) $0.009 l+800=0.011 g$ $\newline$ $l=g$ $\newline$ (B) $0.009 l=0.011 g+800$ $\newline$ $l=g$ $\newline$ (c) $0.009 l=0.011 g$ $\newline$ $l+800=g$ $\newline$ (D) $0.009 l=0.011 g$ $\newline$ $l=g+800$

View step-by-step help

Home

Math Problems

Algebra 1

Solve linear equations with variables on both sides: word problems

Full solution

Q. Liam deposits

l

dollars into an account that earns

0.9 \%

in simple interest each year. Grace deposits

g

dollars into an account that earns

1.1 \%

in simple interest each year. Both Liam and Grace let their money earn interest for one year and make no further deposits. If Liam's initial deposit was

\$ 800

more than Grace's, and if both Liam and Grace earn the same amount of interest after one year, which of the following systems of equations could be used to find their initial deposits?

\newline

Choose

1

answer:

\newline

(A)

0.009 l+800=0.011 g

\newline

l=g

\newline

(B)

0.009 l=0.011 g+800

\newline

l=g

\newline

(c)

0.009 l=0.011 g

\newline

l+800=g

\newline

(D)

0.009 l=0.011 g

\newline

l=g+800

Set Up Equations: Step $1$ : Let's set up the equations based on the information given. Liam's deposit is $l$ dollars and Grace's deposit is $g$ dollars. Liam's deposit is $\$800$ more than Grace's, so we have $l = g + 800$ .
Calculate Interest: Step $2$ : Now, let's calculate the interest earned by both after one year. Liam earns $0.9\%$ interest, so his interest is $0.009l$ . Grace earns $1.1\%$ interest, so her interest is $0.011g$ . They both earn the same amount of interest, so we have $0.009l = 0.011g$ .
Solve Equations: Step $3$ : We now have two equations: $\newline$ $1$ ) $l = g + 800$ $\newline$ $2$ ) $0.009l = 0.011g$ $\newline$ We need to find which answer choice matches our equations.
Check Answer Choices: Step $4$ : Let's check the answer choices. Choice (A) says $0.009l + 800 = 0.011g$ and $l = g$ , which doesn't match our equations. Choice (B) says $0.009l = 0.011g + 800$ and $l = g$ , which also doesn't match. Choice (C) says $0.009l = 0.011g$ and $l + 800 = g$ , which is incorrect. Choice (D) says $0.009l = 0.011g$ and $l = g + 800$ , which matches our equations exactly.