Full solution
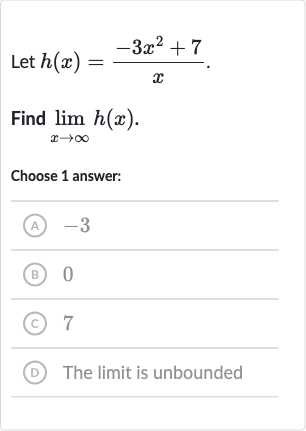
Q. Let .Find .Choose answer:(A) (B) (C) D The limit is unbounded
- Given function: We are given the function . To find the limit as approaches infinity, we need to analyze the behavior of the function as becomes very large.
- Simplifying the function: We can simplify the function by dividing each term in the numerator by , which gives us .
- Analyzing behavior as approaches infinity: As approaches infinity, the term will dominate the behavior of the function because it grows without bound, while the term will approach because the numerator is constant and the denominator grows without bound.
- Dominant term in the limit: Therefore, the limit of as approaches infinity is dominated by the term , which goes to negative infinity. The term , which goes to , does not affect the limit.
- Limit of as approaches infinity: The limit of as approaches infinity is unbounded, and it goes to negative infinity. So the correct answer is (D) The limit is unbounded.