Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

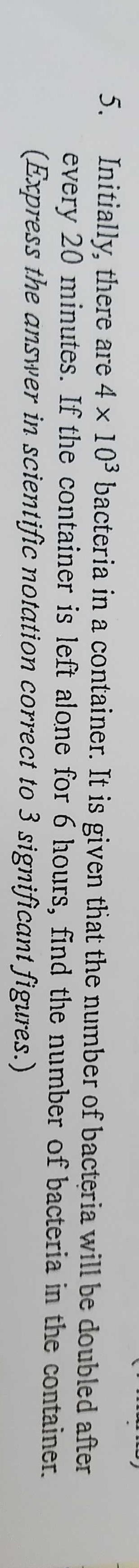
Initially, there are 4×10^(3) bacteria in a container. It is given that the number of bacteria will be doubled after every 20 minutes. If the container is left alone for 6 hours, find the number of bacteria in the container, (Express the answer in scientific notation correct to 3 significant figures.)

Initially, there are 4×103 4 \times 10^{3} bacteria in a container. It is given that the number of bacteria will be doubled after every 2020 minutes. If the container is left alone for 66 hours, find the number of bacteria in the container, (Express the answer in scientific notation correct to 33 significant figures.)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 6right chevron icon
Ratios and rates: word problemsright chevron icon

Full solution

Q. Initially, there are 4×103 4 \times 10^{3} bacteria in a container. It is given that the number of bacteria will be doubled after every 2020 minutes. If the container is left alone for 66 hours, find the number of bacteria in the container, (Express the answer in scientific notation correct to 33 significant figures.)
  1. Calculate Doubling Periods: Calculate the total number of doubling periods in 66 hours. \newline66 hours =360= 360 minutes. \newlineDoubling period =20= 20 minutes. \newlineNumber of periods =360/20=18= 360 / 20 = 18.
  2. Apply Doubling Formula: Apply the doubling formula to find the final number of bacteria.\newlineInitial count = 4×1034\times10^3. \newlineFinal count = Initial count ×2Number of periods\times 2^{\text{Number of periods}}.\newlineFinal count = 4×103×2184\times10^3 \times 2^{18}.
  3. Calculate Final Count: Calculate 2182^{18} and multiply by the initial count.\newline218=2621442^{18} = 262144.\newlineFinal count = 4×103×262144=1048576×1034\times10^3 \times 262144 = 1048576\times10^3.

More problems from Ratios and rates: word problems

Question
Mr. Hansraj wants to find the least number of boxes to be added to get a perfect square. He already has 79247924 boxes with him. How many more boxes are required?\newline(A)819(A)819\newline(B)412(B)412\newline(C)419(C)419\newline(D)176(D)176
Get tutor helpright-arrow

Posted 3 months ago

Question
A lake near the Arctic Circle is covered by sheet of ice during the cold winter months. When spring arrives, the ice starts to melt.\newlineSS models the ice sheet's thickness (in meters) after tt weeks.\newlineS=−0.25t+4S=-0.25t+4\newlineWhat is the ice sheet's thickness at the beginning of spring?\newlinemetersmeters
Get tutor helpright-arrow

Posted 3 months ago

Question
Melanie practices the piano 14351435 minutes in 55 weeks. Assuming she practices the same amount every week, how many minutes would she practice in 44 weeks?\newlineAnswer: minutes
Get tutor helpright-arrow

Posted 3 months ago

Question
Emily practices the piano 595595 minutes in 55 weeks. Assuming she practices the same amount every week, how many minutes would she practice in 44 weeks?\newlineAnswer: minutes
Get tutor helpright-arrow

Posted 3 months ago

Question
Jayden practices the piano 896896 minutes in 44 weeks. Assuming he practices the same amount every week, how many minutes would he practice in 55 weeks?\newlineAnswer: minutes
Get tutor helpright-arrow

Posted 3 months ago

Question
Ai Mi practices the piano 10641064 minutes in 44 weeks. Assuming she practices the same amount every week, how many minutes would she practice in 33 weeks?\newlineAnswer: minutes
Get tutor helpright-arrow

Posted 3 months ago

Question
Which of the following sets of numbers could represent the three sides of a triangle?\newline{12,20,34} \{12,20,34\} \newline{4,6,11} \{4,6,11\} \newline{10,12,21} \{10,12,21\} \newline{13,18,33} \{13,18,33\}
Get tutor helpright-arrow

Posted 3 months ago

Question
Which of the following sets of numbers could represent the three sides of a triangle?\newline{15,26,41} \{15,26,41\} \newline{5,10,16} \{5,10,16\} \newline{13,27,40} \{13,27,40\} \newline{15,27,40} \{15,27,40\}
Get tutor helpright-arrow

Posted 3 months ago

Question
Which of the following sets of numbers could represent the three sides of a triangle?\newline{12,19,31} \{12,19,31\} \newline{10,25,37} \{10,25,37\} \newline{10,15,26} \{10,15,26\} \newline{7,21,27} \{7,21,27\}
Get tutor helpright-arrow

Posted 3 months ago

Question
Which of the following sets of numbers could represent the three sides of a triangle?\newline{4,14,18} \{4,14,18\} \newline{7,11,19} \{7,11,19\} \newline{4,8,10} \{4,8,10\} \newline{10,24,35} \{10,24,35\}
Get tutor helpright-arrow

Posted 3 months ago

View all (68)