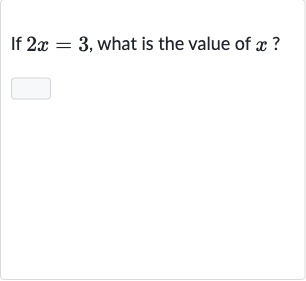AI tutor
Full solution
Q. If , what is the value of ?
- Understand and isolate variable : Understand the equation and isolate the variable .
- Divide by to solve for x: Divide both sides of the equation by to solve for .
- Check for errors in solution: Check the solution for any mathematical errors.