Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

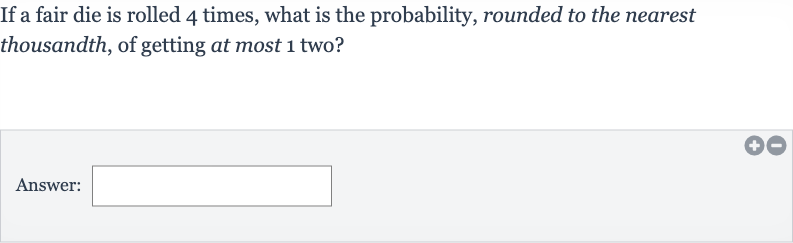
If a fair die is rolled 4 times, what is the probability, rounded to the nearest thousandth, of getting at most 1 two?
Answer:

If a fair die is rolled $4$ times, what is the probability, rounded to the nearest thousandth, of getting at most $1$ two? $\newline$ Answer:

View step-by-step help

View step-by-step help

Probability of independent and dependent events

Full solution

Q. If a fair die is rolled

4

times, what is the probability, rounded to the nearest thousandth, of getting at most

1

two?

\newline

Answer:

Calculate Probability of Not Rolling Two: Determine the probability of not rolling a two on a single die roll. $\newline$ A fair die has $6$ sides, so the probability of rolling any specific number, including a two, is $\frac{1}{6}$ . Therefore, the probability of not rolling a two is $\frac{5}{6}$ .
Calculate Probability of Not Rolling Two in Four Rolls: Calculate the probability of not rolling a two in all four rolls. $\newline$ Since each roll is independent, we multiply the probability of not rolling a two for each roll. $\newline$ $(\frac{5}{6}) \times (\frac{5}{6}) \times (\frac{5}{6}) \times (\frac{5}{6}) = (\frac{5}{6})^4$
Calculate Probability of Rolling Exactly One Two: Calculate the probability of rolling exactly one two in four rolls. $\newline$ We need to consider all the different positions the two can appear in, which is $4$ (first, second, third, or fourth roll). The probability for each scenario is $(1/6)$ for rolling a two and $(5/6)$ for not rolling a two in the other three rolls. $\newline$ $4 \times (1/6) \times (5/6) \times (5/6) \times (5/6) = 4 \times (1/6) \times (5/6)^3$
Add Probabilities of No Twos and Exactly One Two: Add the probabilities of rolling no twos and exactly one two. $\newline$ This will give us the probability of rolling at most one two in four rolls. $\newline$ $(5/6)^4 + 4 \times (1/6) \times (5/6)^3$
Perform Calculations: Perform the calculations. $\newline$ $(\frac{5}{6})^4 = (\frac{625}{1296})$ $\newline$ $4 \times (\frac{1}{6}) \times (\frac{5}{6})^3 = 4 \times (\frac{1}{6}) \times (\frac{125}{216}) = (\frac{500}{1296})$ $\newline$ Adding these together gives: $\newline$ $(\frac{625}{1296}) + (\frac{500}{1296}) = (\frac{1125}{1296})$
Round Result: Round the result to the nearest thousandth. $\frac{1125}{1296} \approx 0.868$

More problems from Probability of independent and dependent events

Question

6

-sided die two times. What is the probability of rolling a number greater than \(3\) and then rolling a number less than \(4\)? Write your answer as a percentage. ____ `%`

Posted 1 month ago

Question

9

college students running for student government class president. The candidates include

7

education majors.

\newline

6

of the candidates are randomly chosen to give the first

6

speeches, what is the probability that all of them are education majors?

\newline

Write your answer as a decimal rounded to four decimal places.

Posted 3 months ago

Question

In an experiment, the probability that event

A

\frac{2}{7}

, the probability that event

B

\frac{7}{9}

, and the probability that events

A

B

\frac{1}{9}

\newline

A

B

independent events?

\newline

\newline

\text{yes}

\newline

\text{no}

Posted 2 months ago

Question

At a science museum, visitors can compete to see who has a faster reaction time. Competitors watch a red screen, and the moment they see it turn from red to green, they push a button. The machine records their reaction times and also asks competitors to report their gender.

\newline

The probability that a competitor reacted in over

0.7

0.6

, the probability that a competitor was female is

0.4

, and the probability that a competitor reacted in over

0.7

seconds and was female is

0.3

\newline

What is the probability that a randomly chosen competitor reacted in over

0.7

seconds or was female?

\newline

Write your answer as a whole number, decimal, or simplified fraction.

\newline

Posted 3 months ago

Question

A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well.

\newline

If the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

Posted 1 month ago

Question

There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____

Posted 3 months ago

Question

There are two different raffles you can enter.

\newline

In raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are

1,000

in the raffle, each costing `$11`.

\newline

Raffle B is for a `$370` prize. Out of

125

tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.

\newline

Which raffle is a better deal?

\newline

\newline

\text{[A]Raffle A}

\newline

\text{[B]Raffle B}

Posted 2 months ago

Question

X

is a normally distributed random variable with mean

49

and standard deviation

25

\newline

What is the probability that

X

24

74

?

\newline

0.68-0.95-0.997

rule and write your answer as a decimal. Round to the nearest thousandth if necessary.

\newline

Posted 3 months ago

Question

X

is a normally distributed random variable with mean

65

and standard deviation

8

\newline

What is the probability that

X

62

68

?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

\newline

Posted 3 months ago

Question

Complete the statement. Round your answer to the nearest thousandth.

\newline

In a population that is normally distributed with mean

43

and standard deviation

3

30\%

of the values are those less than ______.

Posted 3 months ago