Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Given the reference angle of (2pi)/(5), find the corresponding angle in Quadrant 2. Answer:

Given the reference angle of 2π5 \frac{2 \pi}{5} , find the corresponding angle in Quadrant 22.\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Find trigonometric ratios using a Pythagorean or reciprocal identityright chevron icon

Full solution

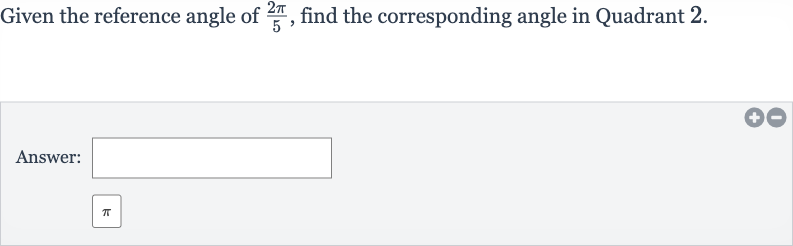
Q. Given the reference angle of 2π5 \frac{2 \pi}{5} , find the corresponding angle in Quadrant 22.\newlineAnswer:
  1. Determine reference angle: Determine the reference angle in radians.
  2. Understand Quadrant 22 angles: Understand that the reference angle is the acute angle that the terminal side of an angle makes with the x-axis. In Quadrant 22, the corresponding angle θ\theta would be π−(reference angle)\pi - (\text{reference angle}) because angles in Quadrant 22 have a measure between π2\frac{\pi}{2} and π\pi.
  3. Calculate angle in Quadrant 22: Calculate the corresponding angle in Quadrant 22 using the reference angle (2π)/(5)(2\pi)/(5).\newlineθ=π−(2π)/(5)\theta = \pi - (2\pi)/(5)
  4. Perform subtraction: Perform the subtraction to find the corresponding angle. \newlineθ=5π5−2π5\theta = \frac{5\pi}{5} - \frac{2\pi}{5}\newlineθ=3π5\theta = \frac{3\pi}{5}

More problems from Find trigonometric ratios using a Pythagorean or reciprocal identity

Question
If cos⁡(θ)=817 \cos(\theta)=\frac{8}{17} and 0∘<θ<90∘ 0^\circ<\theta<90^\circ , what is sec⁡(θ) \sec(\theta) ? Write your answer in simplified, rationalized form. sec⁡(θ)= \sec(\theta)= ______
Get tutor helpright-arrow

Posted 3 months ago

Question
cos⁡(x)=−0.3\cos(x) = -0.3. What is sin⁡(90∘−x)\sin(90^\circ - x)? ____
Get tutor helpright-arrow

Posted 3 months ago

Question
If csc⁡(θ)=178 \csc(\theta) = \frac{17}{8} and 0∘<θ<90∘ 0^\circ < \theta < 90^\circ , what is tan⁡(θ) \tan(\theta) ?\newlineWrite your answer in simplified, rationalized form.\newlinetan⁡(θ)= \tan(\theta) = ______\newline
Get tutor helpright-arrow

Posted 3 months ago

Question
Is the sine function even or odd?\newlineChoices:\newline[A]even\text{[A]even}\newline[B]odd\text{[B]odd}
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the sentence as an equation. \newline8989 is equal to the quotient of yy and 1717 \newlineType a slash ( / / ) if you want to use a division sign. \newline_____
Get tutor helpright-arrow

Posted 2 months ago

Question
Write the sentence as an equation. \newline4545 is equal to the quotient of zz and 55 \newlineType a slash ( / / ) if you want to use a division sign. \newline_____
Get tutor helpright-arrow

Posted 4 months ago

Question
Solve for hh. \newline h2+24h=0h^2 + 24h = 0 \newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas. \newline h=h = _____
Get tutor helpright-arrow

Posted 4 months ago

Question
h2−4h=0h^2 - 4h = 0
Get tutor helpright-arrow

Posted 2 months ago

Question
Combine the like terms to create an equivalent expression:\newline−k−(−8k)=□-k-(-8k)=\square
Get tutor helpright-arrow

Posted 4 months ago

Question
Which of the following degree measures is equal to 5π 5 \pi radians?\newline(The number of degrees of arc in a circle is 360360 . The number of radians of arc in a circle is 2π 2 \pi .)\newlineChoose 11 answer:\newline(A) 144∘ 144^{\circ} \newline(B) 900∘ 900^{\circ} \newline(C) 1,080∘ 1,080^{\circ} \newline(D) 1,800∘ 1,800^{\circ}
Get tutor helpright-arrow

Posted 2 months ago

View all (63)