Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the derivative of the following function.

y=ln(-2x^(3))
Answer:
y^(')=

Find the derivative of the following function. $\newline$ $y=\ln \left(-2 x^{3}\right)$ $\newline$ Answer: $y^{\prime}=$

View step-by-step help

View step-by-step help

Find derivatives using logarithmic differentiation

Full solution

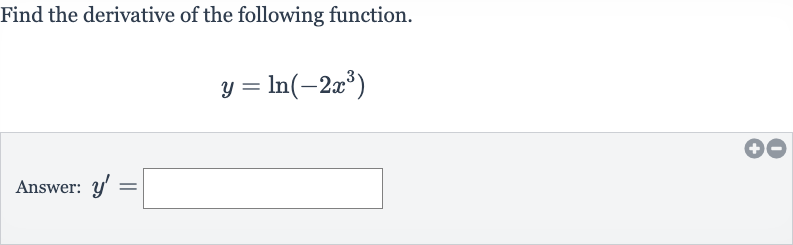
Q. Find the derivative of the following function.

\newline

y=\ln \left(-2 x^{3}\right)

\newline

Answer:

y^{\prime}=

Apply Chain Rule: First, we need to apply the chain rule to differentiate the function $y=\ln(-2x^{3})$ . The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function.
Find Derivative of Inner Function: The outer function is the natural logarithm $\ln(u)$ , and its derivative is $\frac{1}{u}$ . The inner function is $-2x^3$ , and we will find its derivative next.
Apply Chain Rule Again: The derivative of the inner function $-2x^3$ with respect to $x$ is found by using the power rule, which states that the derivative of $x^n$ is $n\cdot x^{(n-1)}$ . So the derivative of $-2x^3$ is $-2\cdot 3\cdot x^{(3-1)} = -6x^2$ .
Simplify Expression: Now we can apply the chain rule. The derivative of $y$ with respect to $x$ is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. This gives us $y' = \frac{1}{-2x^3} \times (-6x^2)$ .
Cancel Common Terms: Simplify the expression by multiplying the two terms. This gives us $y' = \frac{-6x^2}{-2x^3}$ .
Simplify Constant Terms: We can simplify the expression further by canceling out the common terms. The $x^2$ in the numerator and one of the $x$ 's in the denominator cancel out, and the negatives cancel each other. This leaves us with $y' = \frac{6}{2x}$ .
Simplify Constant Terms: We can simplify the expression further by canceling out the common terms. The $x^2$ in the numerator and one of the $x$ 's in the denominator cancel out, and the negatives cancel each other. This leaves us with $y' = \frac{6}{2x}$ .Finally, we can simplify the constant terms. $6$ divided by $2$ is $3$ , so the final simplified derivative is $y' = \frac{3}{x}$ .

More problems from Find derivatives using logarithmic differentiation

Question

\newline

\sqrt{\frac{9}{25}}

\newline

Posted 3 months ago

Question

\newline

1,000

\text{ milligrams}

\_\_\_\_

\text{ grams}

Posted 3 months ago

Question

3

-gallon bottle of bleach costs

\$11.52

. What is the price per quart?

\newline

Posted 3 months ago

Question

Maureen can't wait to make chocolate chip zucchini bread with zucchini from her garden. Her recipe calls for

8

ounces of chocolate chips per loaf. If she has enough zucchini to make

4

loaves of zucchini bread, how many pounds of chocolate chips does she need?

\newline

Hint: There are

16

1

\newline

Write your answer as a whole number, decimal, or simplified fraction. Do not round.

\newline

Posted 3 months ago

Question

A whale is swimming due north at a speed of

30

miles per hour. Just

5

miles away, a whale-watching tour boat is traveling south, directly toward the whale, at a speed of

46

miles per hour. How long will it be before they meet? If necessary, round your answer to the nearest minute.

\_\_\_\_

\_\_\_\_

Posted 3 months ago

Question

\newline

500

=

Posted 4 months ago

Question

\newline

2,000

=

Posted 4 months ago

Question

\newline

750

=

Posted 4 months ago

Question

\newline

1,500

=

Posted 4 months ago

Question

\newline

1,500

=

Posted 4 months ago