Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify.
((2m^(2))/(3m^(-1)))^(2)
Write your answer using only positive exponents.

Simplify. $\newline$ $\left(\frac{2 m^{2}}{3 m^{-1}}\right)^{2}$ $\newline$ Write your answer using only positive exponents.

View step-by-step help

View step-by-step help

Full solution

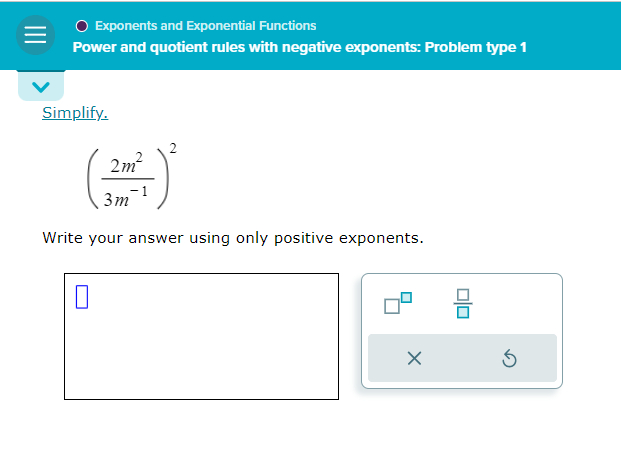
Q. Simplify.

\newline

\left(\frac{2 m^{2}}{3 m^{-1}}\right)^{2}

\newline

Write your answer using only positive exponents.

Simplify base: We have the expression $((2m^{2})/(3m^{-1}))^{2}$ . Let's first simplify the base by applying the quotient rule for exponents, which states that $a^{m}/a^{n} = a^{m-n}$ when $a$ is not equal to $0$ . $\newline$ $((2m^{2})/(3m^{-1}))^{2} = ((2/3) * (m^{2} * m^{1}))^{2}$
Combine exponents on $m$ : Now, we combine the exponents on $m$ by adding them because when you multiply with the same base, you add the exponents. $\left(\frac{2}{3} \cdot m^{2+1}\right)^{2} = \left(\frac{2}{3} \cdot m^{3}\right)^{2}$
Apply power rule: Next, we apply the power rule for exponents, which states that $(a*b)^n = a^n * b^n$ . $((2/3) * m^{3})^{2} = (2/3)^{2} * (m^{3})^{2}$
Square the fraction: Now, we simplify each part separately. First, we square the fraction $(\frac{2}{3})$ . $\left(\frac{2}{3}\right)^{2} = \left(2^{2}\right)/\left(3^{2}\right) = \frac{4}{9}$
Square the $m$ term: Then, we square the $m$ term. $(m^{3})^{2} = m^{3*2} = m^{6}$
Multiply results: Finally, we multiply the results together to get the simplified expression with only positive exponents. $\frac{4}{9} \times m^{6}$

More problems from Power rule

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 3 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 3 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 2 months ago

Question

\newline

32^{(-1/5)}

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 3 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 2 months ago