Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Expand the logarithm fully using the properties of logs. Express the final answer in terms of log x,log y, and log z. log ((y^(5)root(3)(z))/(x^(2))) Answer:

Expand the logarithm fully using the properties of logs. Express the final answer in terms of log⁡x,log⁡y \log x, \log y , and log⁡z \log z .\newlinelog⁡y5z3x2 \log \frac{y^{5} \sqrt[3]{z}}{x^{2}} \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Quotient property of logarithmsright chevron icon

Full solution

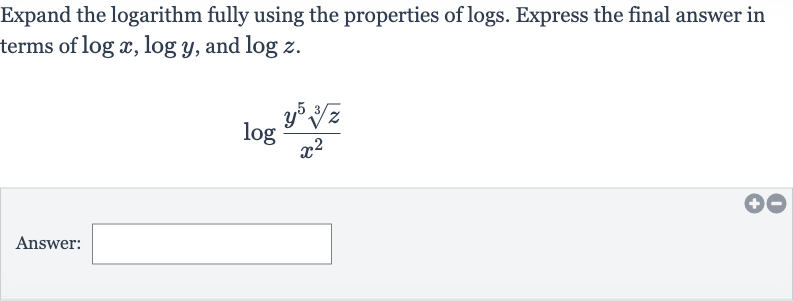
Q. Expand the logarithm fully using the properties of logs. Express the final answer in terms of log⁡x,log⁡y \log x, \log y , and log⁡z \log z .\newlinelog⁡y5z3x2 \log \frac{y^{5} \sqrt[3]{z}}{x^{2}} \newlineAnswer:
  1. Identify Properties: Identify the properties used to expand the logarithm.\newlineWe will use the quotient property of logarithms to separate the numerator and the denominator, the power property to bring the exponents in front of the logs, and the root property to express the cube root as a fractional exponent.
  2. Apply Quotient Property: Apply the quotient property to the logarithm.\newlineThe quotient property of logarithms states that log⁡b(PQ)=log⁡b(P)−log⁡b(Q)\log_b\left(\frac{P}{Q}\right) = \log_b(P) - \log_b(Q). We apply this to log⁡(y5z3x2)\log\left(\frac{y^{5}\sqrt[3]{z}}{x^{2}}\right) to get:\newlinelog⁡(y5z3)−log⁡(x2)\log(y^{5}\sqrt[3]{z}) - \log(x^{2})
  3. Apply Power Property: Apply the power property to the logarithms.\newlineThe power property of logarithms states that log⁡b(Pk)=klog⁡b(P)\log_b(P^k) = k\log_b(P). We apply this to both terms:\newline5log⁡(y)+log⁡(z13)−2log⁡(x)5\log(y) + \log(z^{\frac{1}{3}}) - 2\log(x)
  4. Apply Root Property: Apply the root property to the logarithm of zz. The cube root of zz can be written as z(1/3)z^{(1/3)}, so we have already applied the root property when we wrote log⁡(z(1/3))\log(z^{(1/3)}) in the previous step.
  5. Combine Results: Combine the results to get the final expanded form.\newlineThe final expanded form of the logarithm is:\newline5log⁡(y)+(13)log⁡(z)−2log⁡(x)5\log(y) + \left(\frac{1}{3}\right)\log(z) - 2\log(x)

More problems from Quotient property of logarithms

Question
Write the exponential equation in logarithmic form.\newline93=7299^3 = 729\newlinelog⁡□729=3\log_\square 729 = 3
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the exponential equation in logarithmic form.\newlinee4≈54.598e^4 \approx 54.598\newlineln⁡____≈4\ln\_\_\_\_ \approx 4
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the logarithmic equation in exponential form.\newlinelog⁡10100=2\log_{10}100 = 2\newline102=‾10^2 = \underline{\hspace{2em}}
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate. Write your answer as a whole number, proper fraction, or improper fraction in simplest form.\newlineln⁡(e)10=\frac{\ln (e)}{10} = ______
Get tutor helpright-arrow

Posted 3 months ago

Question
Rewrite as a quotient of two common logarithms. Write your answer in simplest form.\newlinelog⁡333=\log_3 33 = ______
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate. Round your answer to the nearest thousandth.\newlinelog⁡550=\log_{5}50 = ____
Get tutor helpright-arrow

Posted 3 months ago

Question
Which property of logarithms does this equation demonstrate? \newlinelog⁡33+log⁡36=log⁡318\log_3 3 + \log_3 6 = \log_3 18\newlineChoices:\newline(A) Product Property\text{Product Property}\newline(B) Power Property\text{Power Property}\newline(C) Quotient Property\text{Quotient Property}
Get tutor helpright-arrow

Posted 3 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡(uv)\log(uv)\newline_____
Get tutor helpright-arrow

Posted 3 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡v7\log v^7 \newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of base-66 logarithms or multiples of base-66 logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡6w6\log_6 w^6\newline______
Get tutor helpright-arrow

Posted 3 months ago

View all (63)