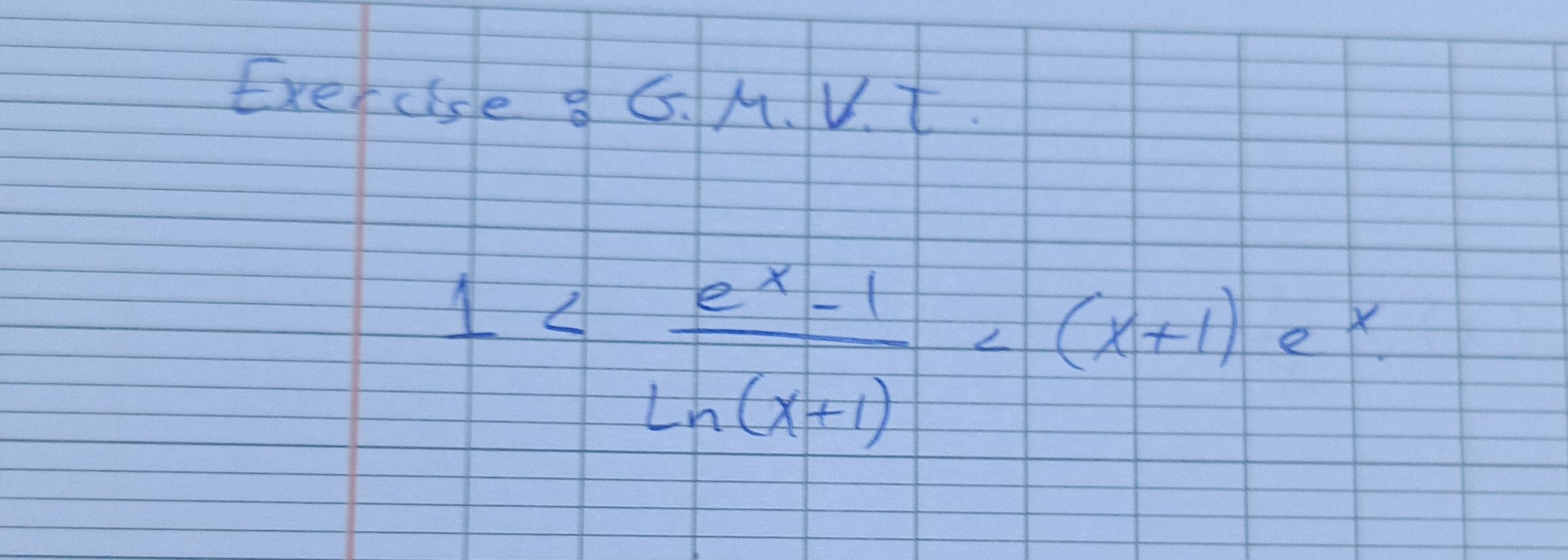Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Exercise: G.M.V.T.

1 < (e^(x)-1)/(ln(x+1)) < (x+1)e^(x)

Exercise: G.M.V.T. $\newline$ $1<\frac{e^{x}-1}{\ln (x+1)}<(x+1) e^{x}$

View step-by-step help

View step-by-step help

Solve advanced linear inequalities

Full solution

Q. Exercise: G.M.V.T.

\newline

1<\frac{e^{x}-1}{\ln (x+1)}<(x+1) e^{x}

Understand Given Inequality: First, we need to understand the given inequality $1 < \frac{e^{x}-1}{\ln(x+1)} < (x+1)e^{x}$ . We have a compound inequality which means we need to solve two separate inequalities: $\frac{e^{x}-1}{\ln(x+1)} > 1$ and $\frac{e^{x}-1}{\ln(x+1)} < (x+1)e^{x}$ .
Solve First Inequality: Let's start with the first inequality $(e^{x}-1)/(\ln(x+1)) > 1$ . To solve this, we can multiply both sides by $\ln(x+1)$ to get rid of the denominator, assuming $\ln(x+1)$ is positive (which it is for $x > 0$ since $\ln(1) = 0$ and $\ln(x)$ is increasing for $x > 0$ ). $\newline$ $(e^{x}-1) > \ln(x+1)$
Check Behavior at Infinity: Now we need to solve $e^{x}-1 > \ln(x+1)$ . This is a transcendental inequality and cannot be solved algebraically. We would typically use numerical methods or graphing to find the solution set for $x$ . However, we can check for obvious solutions or intersections by evaluating the functions at certain points or using properties of $e^{x}$ and $\ln(x)$ .
Consider Second Inequality: Let's check the behavior of the functions as $x$ approaches infinity. As $x$ approaches infinity, $e^{x}$ grows much faster than $\ln(x+1)$ , so the inequality will hold for large values of $x$ . Similarly, as $x$ approaches $0$ from the right, $e^{x}$ approaches $1$ and $\ln(x+1)$ approaches $0$ , so the inequality will not hold near $x$ $1$ .
Simplify Second Inequality: Now let's consider the second inequality $(e^{x}-1)/(\ln(x+1)) < (x+1)e^{x}$ . We can start by multiplying both sides by $\ln(x+1)$ to get rid of the denominator, again assuming $\ln(x+1)$ is positive. $\newline$ $e^{x}-1 < (x+1)e^{x} \cdot \ln(x+1)$
Subtract Terms: Simplify the inequality by distributing $(x+1)e^{x}$ on the right side. $e^{x}-1 < x e^{x} \ln(x+1) + e^{x} \ln(x+1)$
Combine Like Terms: Subtract $e^{x}$ from both sides to bring terms involving $e^{x}$ to one side. $\newline$ $-1 < x imes e^{x} imes ext{ln}(x+1) + e^{x} imes ext{ln}(x+1) - e^{x}$
Analyze Behavior Near Zero: Combine like terms on the right side. $\newline$ $-1 < x\cdot e^{x}\cdot \ln(x+1) + (\ln(x+1) - 1)\cdot e^{x}$
Find Exact Solution: This inequality is also transcendental and cannot be solved algebraically. We would again use numerical methods or graphing to find the solution set for $x$ . We can look for intersections and behavior at infinity. As $x$ approaches infinity, the right side grows without bound, so the inequality will hold. Near $x = 0$ , the right side is negative because $\ln(x+1) - 1$ is negative, so the inequality does not hold.
Find Exact Solution: This inequality is also transcendental and cannot be solved algebraically. We would again use numerical methods or graphing to find the solution set for $x$ . We can look for intersections and behavior at infinity. As $x$ approaches infinity, the right side grows without bound, so the inequality will hold. Near $x = 0$ , the right side is negative because $\ln(x+1) - 1$ is negative, so the inequality does not hold.To find the exact range of $x$ that satisfies both inequalities, we would need to graph both sides of each inequality and look for the intervals where the inequalities hold. This is not something that can be done algebraically, and it requires numerical or graphical analysis.

More problems from Solve advanced linear inequalities

Question

-2 x+b y=59

\newline

5 x-y=1

\newline

If the system of equations has exactly one solution

(x, y)

x=2

, what is the value of

b

Posted 2 months ago

Question

\newline

\frac{\sqrt[3]{2}}{\sqrt[3]{-128}}=

Posted 6 days ago

Question

\newline

\frac{\sqrt[4]{2}}{\sqrt[4]{162}}=

Posted 3 months ago

Question

\newline

\sqrt[5]{-16} \cdot 2^{\frac{1}{5}}=

Posted 2 months ago

Question

y

\newline

\begin{array}{l} \frac{y-1}{3 y+7}=\frac{1}{10} \\ y=\square \end{array}

Posted 3 months ago

Question

x

\newline

Your answer must be simplified.

\newline

-30<\frac{x}{-4}

Posted 2 months ago

Question

x

\newline

Your answer must be simplified.

\newline

-36+x<8

Posted 2 months ago

Question

x

\newline

Your answer must be simplified.

\newline

2 x<15

Posted 3 months ago

Question

x

\newline

Your answer must be simplified.

\newline

x-6 \leq 3

Posted 1 month ago

Question

x

\newline

Your answer must be simplified.

\newline

7>\frac{x}{4}

Posted 3 months ago