Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

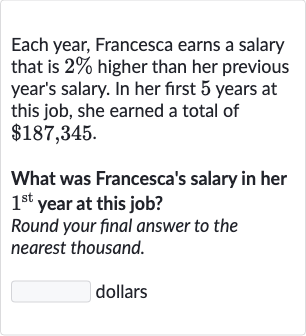
Each year, Francesca earns a salary that is
2% higher than her previous year's salary. In her first 5 years at this job, she earned a total of
$187,345.
What was Francesca's salary in her
1^("st ") year at this job?
Round your final answer to the nearest thousand.

◻ dollars

Each year, Francesca earns a salary that is $2 \%$ higher than her previous year's salary. In her first $5$ years at this job, she earned a total of $\$ 187,345$ . $\newline$ What was Francesca's salary in her $1^{\text {st }}$ year at this job? $\newline$ Round your final answer to the nearest thousand. $\newline$ $\square$ dollars

View step-by-step help

View step-by-step help

Percent of change: word problems

Full solution

Q. Each year, Francesca earns a salary that is

2 \%

higher than her previous year's salary. In her first

5

years at this job, she earned a total of

\$ 187,345

.

\newline

What was Francesca's salary in her

1^{\text {st }}

year at this job?

\newline

Round your final answer to the nearest thousand.

\newline

\square

dollars

Francesca's Salary Increase: Francesca's salary increases by $2\%$ each year. Let's call her first year's salary $S$ . Each year, her salary becomes $1.02$ times the previous year's salary.
Total Salary Calculation: The total salary over $5$ years can be expressed as: $S + S(1.02) + S(1.02)^2 + S(1.02)^3 + S(1.02)^4$ .
Equation Setup: We know the total of these $5$ terms is $\$187,345$ . So, we set up the equation: $S(1 + 1.02 + 1.02^2 + 1.02^3 + 1.02^4) = 187,345$ .
Geometric Series Sum: Calculate the sum of the geometric series: $1 + 1.02 + 1.02^2 + 1.02^3 + 1.02^4$ .
Equation Simplification: The sum is approximately $5.10408$ . So, the equation becomes $S \times 5.10408 = 187,345$ .
Solving for S: Divide both sides by $5.10408$ to solve for $S$ : $S = \frac{187,345}{5.10408}$ .
Division Calculation: Perform the division: $S \approx 187,345 / 5.10408 \approx 36,710$ . But we need to round to the nearest thousand.
Rounding Solution: Rounding $36,710$ to the nearest thousand gives us $\$37,000$ .

More problems from Percent of change: word problems

Question

70\%

\$10?

\newline

\$

Posted 3 months ago

Question

90\%

40

Posted 3 months ago

Question

What is the percent of change from

12

21

\newline

\newline

75 \%

\newline

9\%

\newline

75\%

\newline

9\%

Posted 3 months ago

Question

17

a prime number or a composite number?

\newline

\newline

(A) prime number

\newline

(B) composite number

Posted 2 months ago

Question

28

is what percent of

50 ?

\newline

\%

Posted 4 months ago

Question

2 \%

50

Posted 4 months ago

Question

12

60 \%

of what number?

Posted 4 months ago

Question

24

75 \%

of what number?

Posted 4 months ago

Question

84 \%

300

Posted 3 months ago

Question

15

is what percent of

25 ?

\newline

\%

Posted 4 months ago