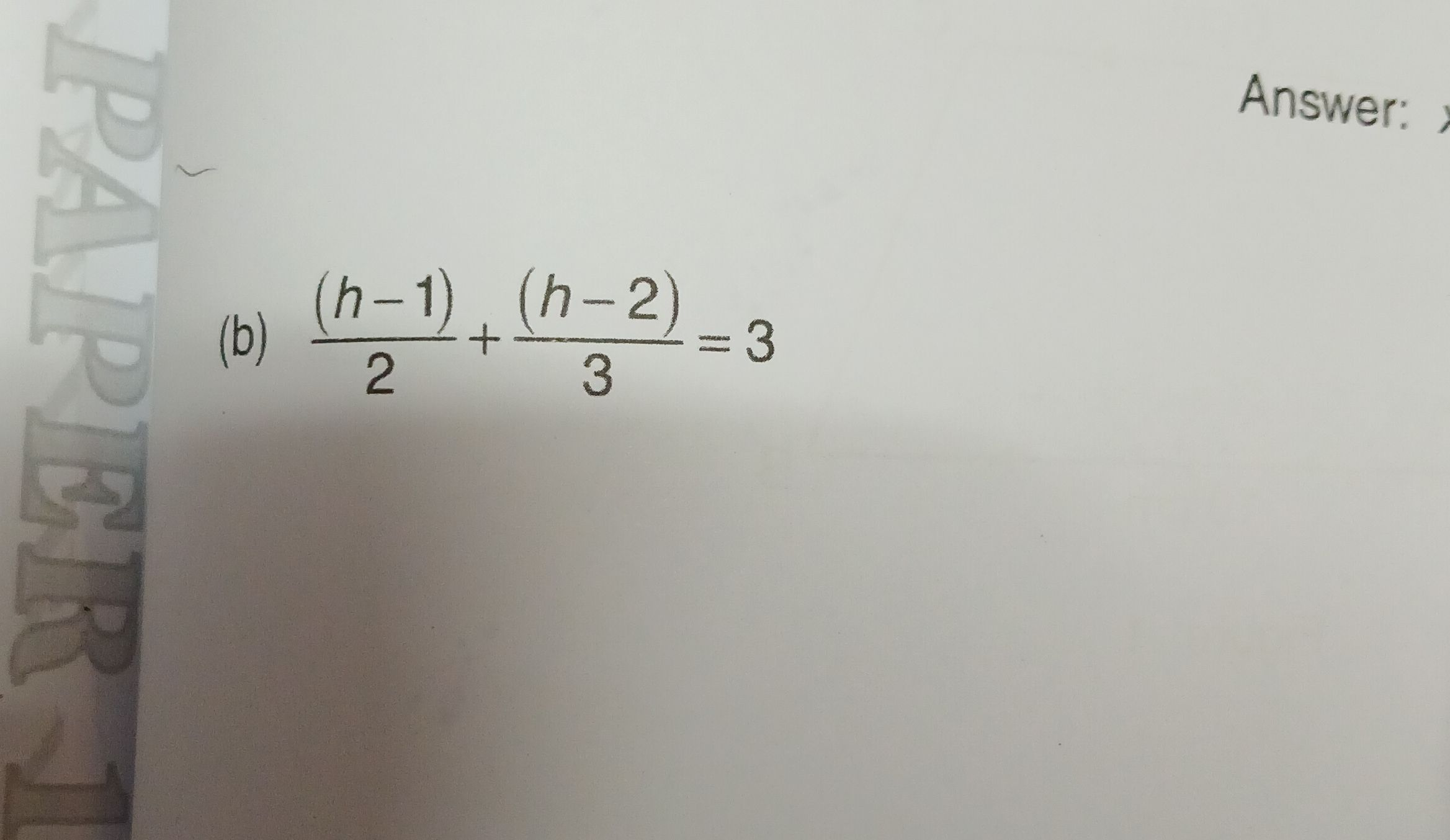AI tutor
Full solution
Q. Answer:(b)
- Find Common Denominator: Find a common denominator for the fractions on the left side of the equation.The common denominator for and is .
- Rewrite Fractions: Rewrite each fraction with the common denominator.This becomes
- Combine Fractions: Combine the fractions on the left side since they have the same denominator.
- Distribute and Combine: Distribute the numerators and combine like terms. This simplifies to
- Eliminate Denominator: Multiply both sides of the equation by to eliminate the denominator.This simplifies to
- Isolate h Term: Add to both sides of the equation to isolate the term with . This simplifies to
- Solve for : Divide both sides by to solve for .This simplifies to
More problems from Solve quadratic inequalities
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help